Thermistor selection
As part of the design challenge I received 10 different thermistors:
213860-1637 NTC Ring Thermistor, 10 kΩ, 1% Tolerance
213860-2637 NTC Ring Thermistor, 10 kΩ, 2% Tolerance
213862-2637 NTC Ring Thermistor, 10 kΩ, 2% Tolerance
215272-3307. Thermistor NTC, 3892K, 3 kΩ, 1% Tolerance
215272-3407. Thermistor NTC, 3892K, 4.7 kΩ, 1% Tolerance
215272-3507. Thermistor NTC, 3892K, 5 kΩ, 1% Tolerance
215272-3607. Thermistor NTC, 3892K, 10 kΩ, 1% Tolerance
215272-3707. Thermistor NTC, 3892K, 12 kΩ, 1% Tolerance
215272-3807. Thermistor NTC, 3892K, 30 kΩ, 1% Tolerance
215272-3907. Thermistor NTC, 3892K, 47 kΩ, 1% Tolerance
And even though any of them could have been used for the experiment, I had to chose one. I ended up selecting the 213860-1637 ring thermistor because the ring made it easier to tighten it, and was the only ring thermistor with a 1% tolerance. One drawback of the ring thermistors is that the package has higher thermal capacity and for the same reason takes longer to react to temperature changes.
Temperature computation
Thermistor are resistors that are very sensitive to the temperature. They can be divided into positive temperature coefficient (PTC) and negative temperature coefficient (NTC) thermistors. A rise of temperature causes an increase of the resistance of a PTC thermistor and a drop of resistance of an NTC thermistor. The datasheet of the 213860-1637 specifies that it is an 10 kΩ ± 1% (25 °C) NTC thermistor with a B of 3500. And that's all that we need to convert the resistance into temperature, using the following equation:
Where:
T0 is the reference temperature (25 + 273.15 °K)
R0 is the resistance resistance at the reference temperature (10 kΩ)
R is the measured resistance in Ω
T is the thermistor temperature in Kelvin
Besides the equations parameters, Molex also provides us a temperature-resistance table in case that we want to use an equations that fits better the values.

The classic Steinhart-Hart equation is:
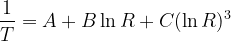
Where A, B, C are terms specific to the thermistors. Since these Molex does not provide them, they could be derived empirically (ideally) or using the provided table. Through the least squares method I found the term values to be:
A = 9.03503079e-04
B = 2.53405800e-04
C = 1.47049465e-07
Lets see how the provided equation compares to the one with the optimized parameters:

With the exception of extreme temperatures, the differences appear to be small.
One interesting thing of the "classic" Steinhart-Hart equation is that it does not include a squared logarithm term. This is because this term usually is too small and doesn't not improve the fitting much, but of course, the more terms that are used, the better the fit.
To keep things simple I just sticked to the classic Steinhart-Hart
