In this post, I will talk about my experiments with the TDK USSM that are aimed at checking out how precisely and how far the ball position can be detected

Setup

To conduct the experiments, a reference line approximately 3 meters in length was drawn, with markings at 20-centimeter intervals. It is assumed that the sensor exhibits isotropic behavior, i.e., identical performance in all directions. However, to ensure consistency across trials, a reference mark was applied to the sensor to maintain the same orientation. The basketball was suspended from the ceiling, positioned directly above the center of the marked grid. The testbed is shown in picture below

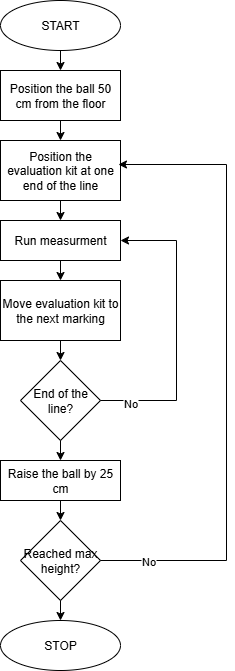
I moved the USSM over the different positions on the grid. For each position, I took a screenshot of the envelop and took note of the detected distance. The test procedure is shown in the following flowchart

Results

Here is the result of the experiments

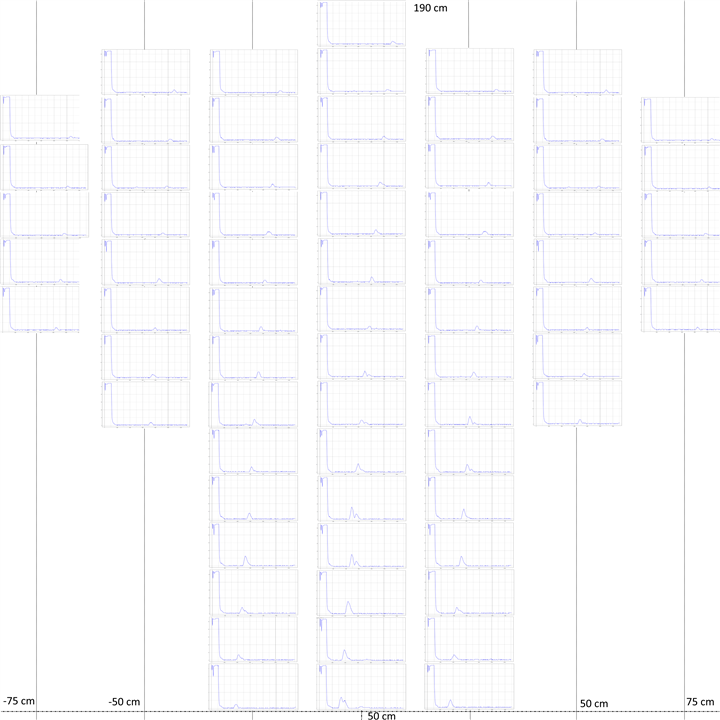
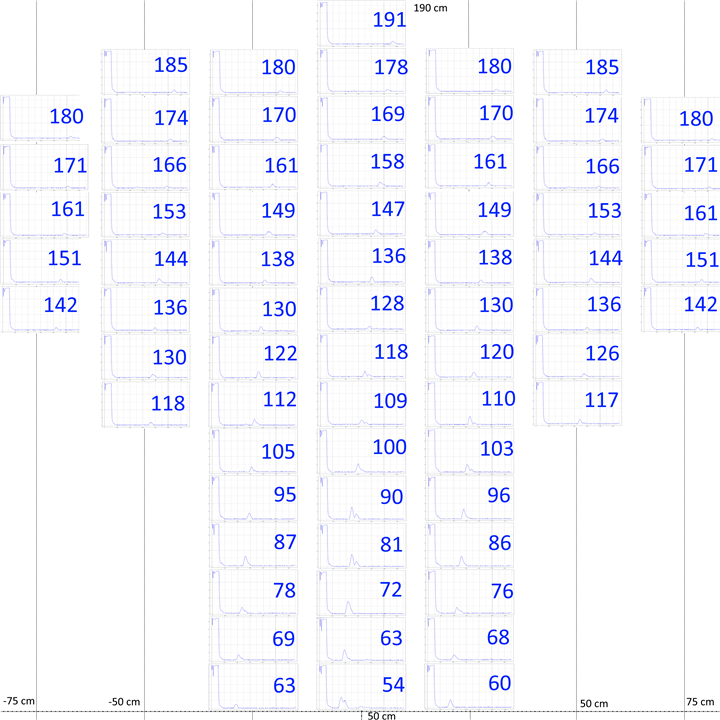
And here is the same diagram with the distances measured by the USSM

The area where the basketball is detected has approximately this shape

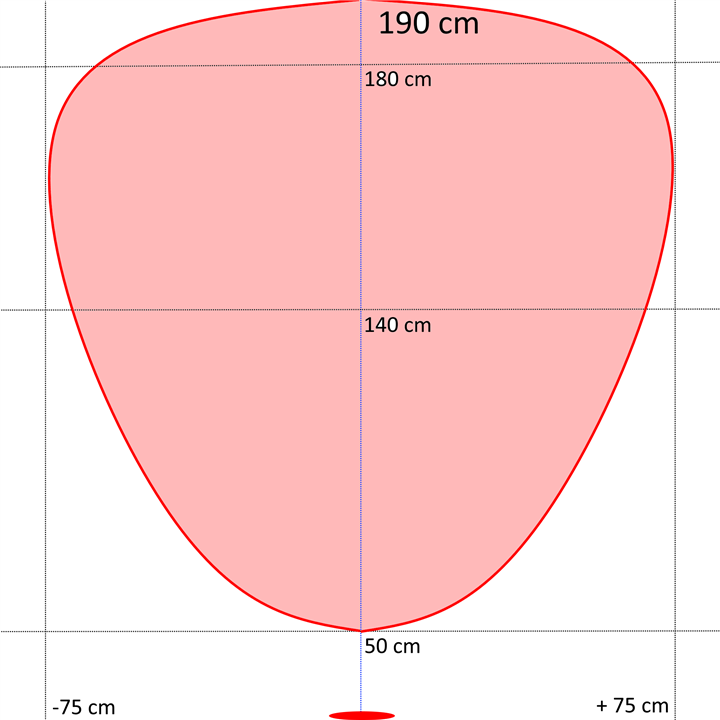
The sensors has a "field of view" of about 25 degrees on each side

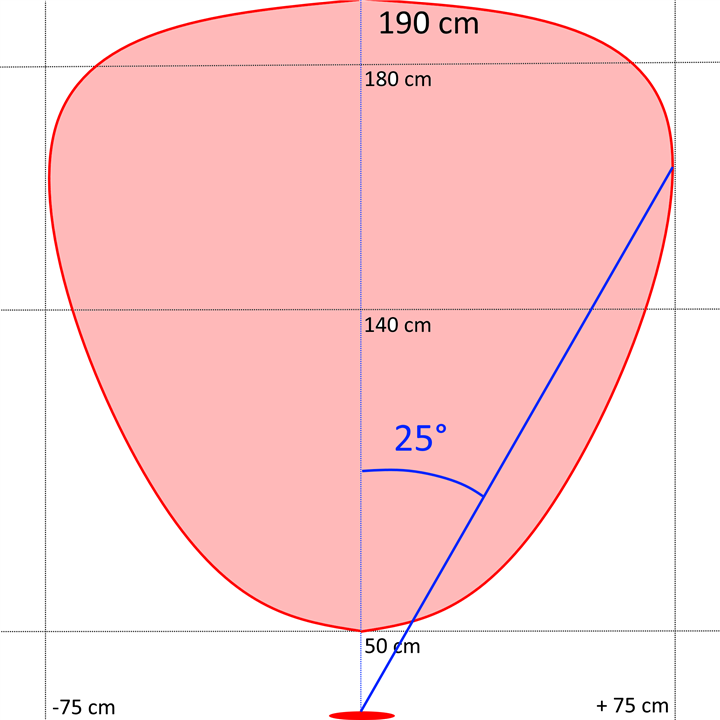
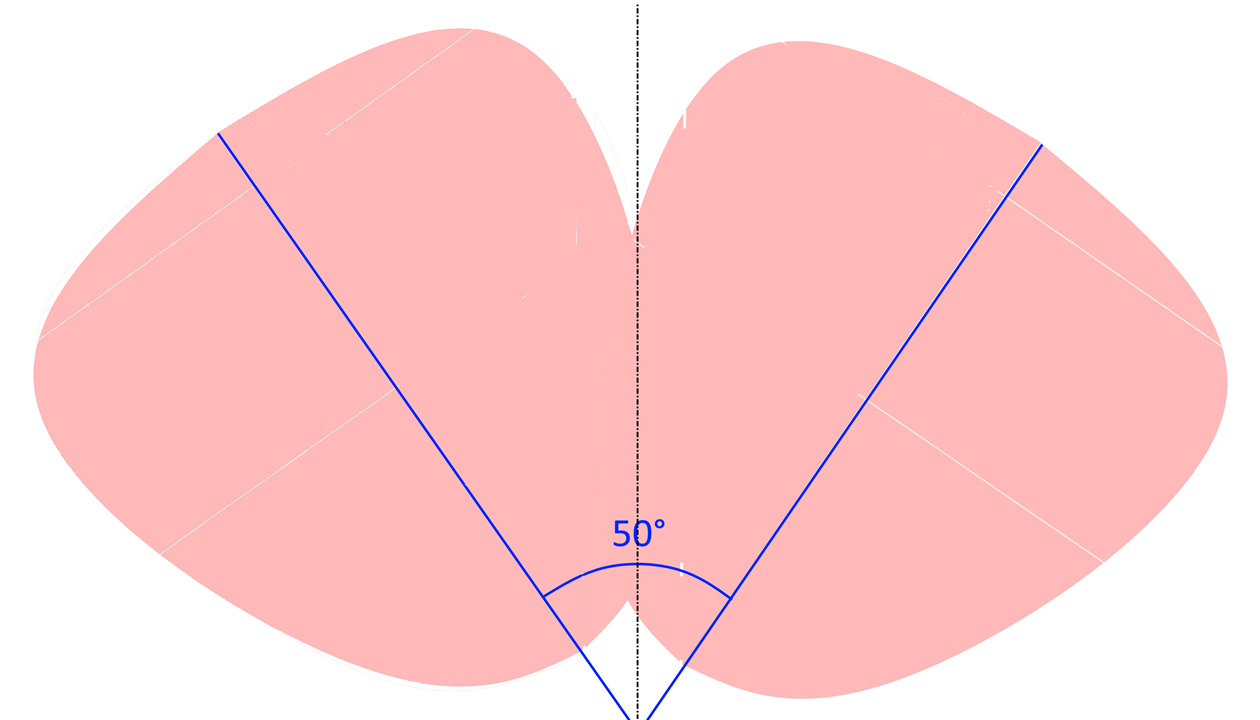
So I think the optimal angle between the sensors is about 50 degrees

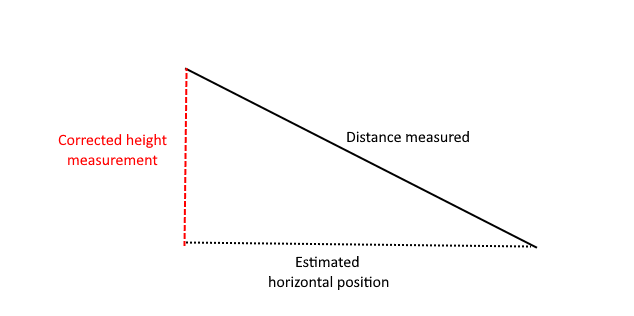
Given the shape of the covered area, I can also correct the distance measurement to take into account the horizontal offset of the ball. The algorithm I have in mind is quite simple (it applies to the two USSMs). 

1. When all the samples have been collected, I calculate the average height of the basketball
2. Given the average height, I can estimate the width of the covered area at that specific distance. I can simply store the width of the covered area at different heights, and interpolate to get an approximation of the area width
3. The horizontal distance between samples (I will call it "step") can be calculated as the width of the covered area divided by the number of samples
4. An horizontal position can now be assigned to each sample

Samples taken by the left USSM, will have negative values for the horizontal position

1. 1st sample will have an horizontal position equal to  - step * (num samples - 1)
2. 2nd sample will have an horizontal position equal to  - step * (num samples - 2)
3. ...
4. last sample will have an horizontal position equal to 0

Samples taken by the right USSM, will have positive values for the horizontal position

1. 1st sample will have an horizontal position equal to 0
2. 2nd sample will have an horizontal position equal to  + step * 1
3. ...
4. last sample will have an horizontal position equal to + step * (num samples - 1)

Now, with a known horizontal position, I can correct the measured distance using the Pitagora theorem

Next steps

With less than a month left and so much work to do, it's time to start writing code and see if I can interface with the USSM. Stay tuned!