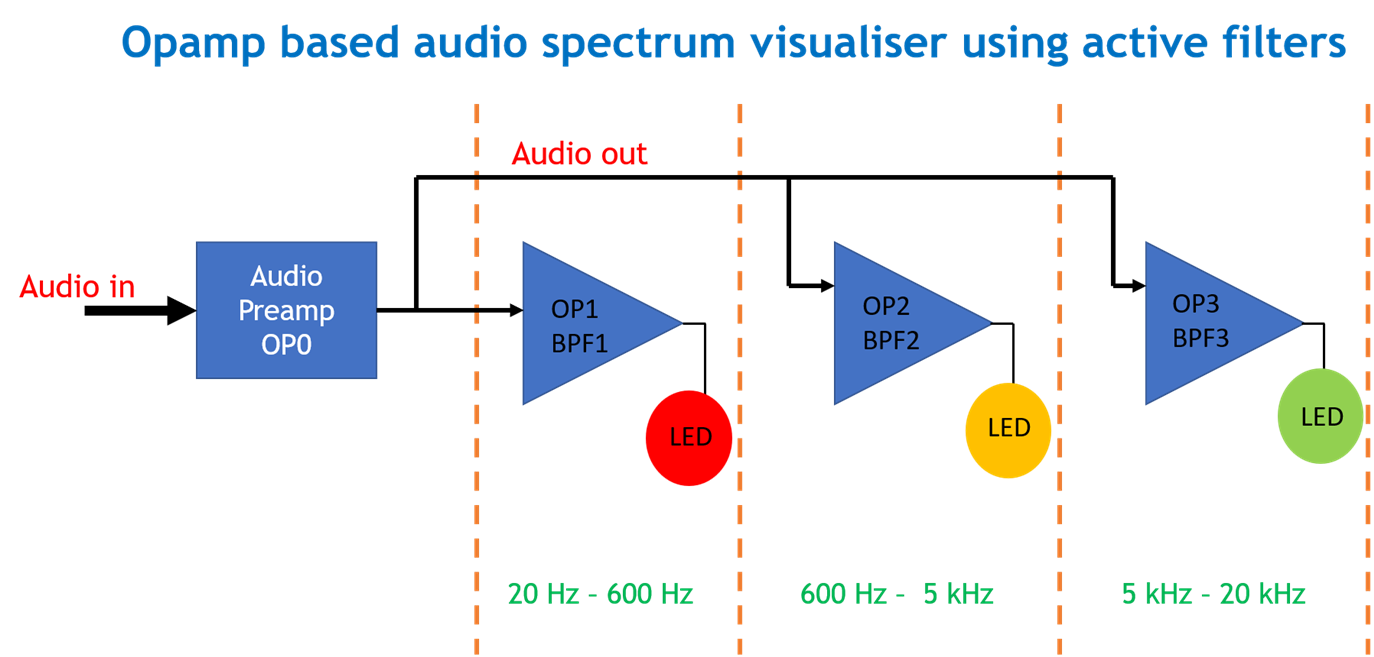
In my last blog (part 1) I introduced the overall idea of the project. The idea was to split the audio spectrum from 20 Hz to 20 kHz using three active filters and each filter's output is connected to LEDs thereby making a LED music visualizer. I also simulated 3 basic filters (LPF,BPF, and HPF) and an active low pass filter to demonstrate the working of active filters.
In this blog, I will do the calculations for the values of the components required to build the active filters and run some simulations before the final hardware build of the circuit. I will be using RC filters with Butterworth response.
The first block in the design is the pre-amplifier. A pre-amp is needed as I'm planning to use the audio out of a smartphone which is in the range of few millivolts. This signal needs to be amplified such that it can be fed to the three opamp filters.
The preamp is a very basic non-inverting opamp amplifier with a voltage gain of about 4-5.
Next, step is to decide the bands for the filters.
Audio Bands
First, the audio signal (20 Hz - 20 kHz) is split into three bands as follows-
| Band | Frequency |
| Band 1 | 20 Hz - 480 Hz |
| Band 2 | 480 Hz - 3 kHz |
| Band 3 | 3 kHz - 20 kHz |
Since the audio spectrum is limited to 20 Hz - 20 kHz, the first band can be filtered out using a low pass filter with a cutoff freq of 480 Hz, this LPF will allow all the frequencies from 20Hz to 480 Hz and attenuate the frequencies above 480 Hz. This low-frequency spectrum of the audio is also known as "Bass". For band 2, a band pass filter is designed such that it can filter out the 480 Hz - 3 kHz band. This band mostly contains the voice or "vocals". Lastly, for band 3, a high pass filter is used with a cutoff freq of 3 kHz meaning that it will attenuate all signals below 3 kHz. This band is also known as "treble".
Now that we have decided on the bands, let's move to filter design.
Filter Design
Active Low Pass Filter
In the last blog, I briefly introduced the active low pass filter circuit. Considering the same circuit and as decided from the above table, Band 1 means a cutoff freq. of 480 Hz, which means fc = 1/(2*pi*R*C) = 480 Hz. Since we have a huge range of standard resistors available but the range of capacitors is limited, a standard value of C is chosen which is 0.1 uF.
By doing the calculations, the value of R is found to be 3315.72 ohms, so the closest standard value for R is chosen as 3.3 kohms.
Hence, design values for the active LPF are R = 3.3k and C = 0.1 uF. This gives the cutoff freq. of 482 Hz which is quite near to the actual cutoff freq.
Now, to set the gain of the filter, a nominal gain of about 2-3 works fine. For calculating the resistor values for gain, the simple gain formula for non-inverting opamp is used.
Active Band Pass Filter
Next, a band pass filter is designed. A band pass filter filters out a band of frequencies which means it has two cutoff freqs, the lower cutoff (fc1) and the higher cutoff (fc2). Here, from the table, fc1 = 480 Hz and fc2 = 3 kHz.
Hence, using the same formula of LPF, the R and C values for fc1 and fc2 are found to be R1 = 500 ohms and C1 = 0.1 uF and R2 = 3.3k and C2 = 0.1uF. This will give the values of fc1 = 3.18 kHz and fc2 = 482 Hz.
Active High Pass Filter
For the last block, a high pass filter is designed. The formula remains the same. The fc for HPF from the table is fc = 3kHz. The values for R and C are decided as R = 500 ohms and C = 0.1 uF.
Simulation Results
I simulated the entire circuit in LT spice to check if it works properly. The simulation setup is AC analysis to check the filter response. The opamps work on a dual rail power supply of +/- 3V. For simulating the audio signal, I have used an AC source.
The below image shows the final circuit diagram along with the individual blocks labeled.
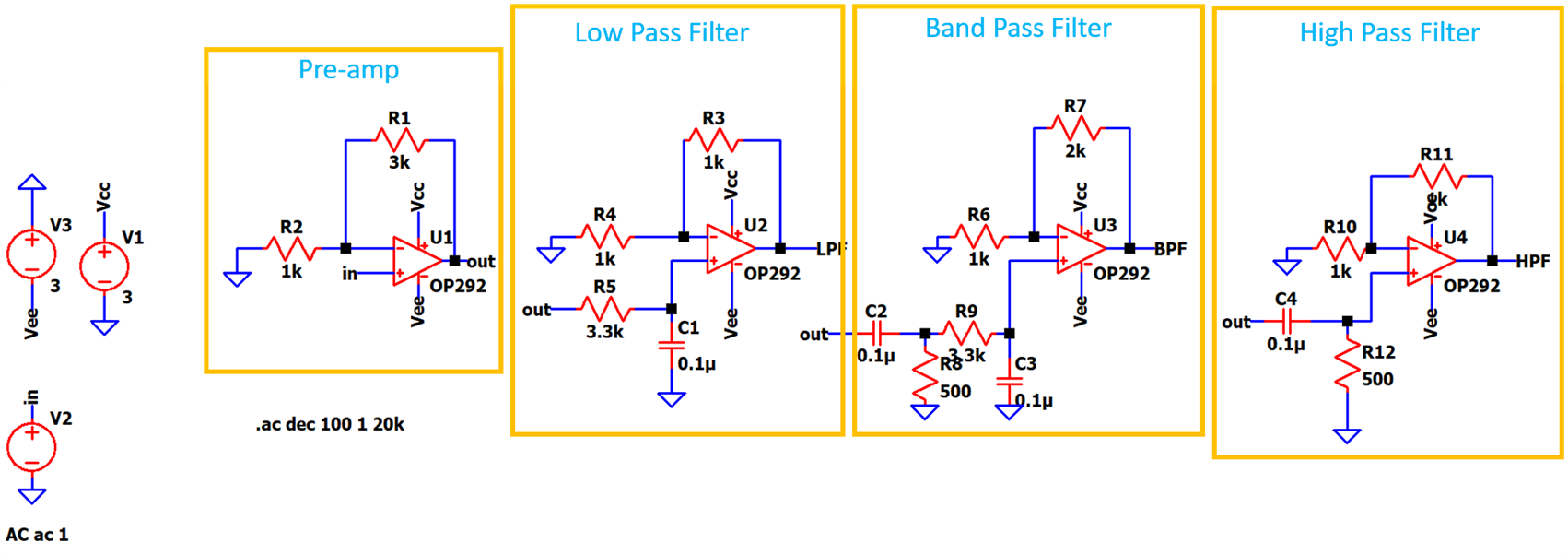
The preamp gives a voltage gain of 4 (non-inverting configuration) and the signal from the output of this preamp is then fed to three filter blocks. The outputs of these filters are connected to LEDs(not shown in Ltspice).
Below are the simulation results -

It can be seen from the frequency response plots, that the filters are working correctly. If we compare the results of the active LPF with the passive LPF from my last blog, it can be seen that here the gain of the active LPF is around 18dB whereas in the case of the passive filter it was around 0dB due to the lossy filter components and no active components to amplify the filtered signal. The same is the case for other filters too.
Another thing to note is that due to the presence of two resistors in BPF, the gain is less due to loss in resistors. This can be compensated by adjusting the gain of the opamp of the BPF block.
In the next blog, I will construct the circuit on a breadboard and publish the results along with the video. Stay tuned!

Top Comments