Background
For handwritten digit recognition, Convolutional Neural Networks (CNNs) are the most effective type of neural network, as they excel at identifying patterns and spatial hierarchies in image data. CNNs have become the standard approach, especially for datasets like MNIST, which contains thousands of labeled images of handwritten digits (0-9) in a 28x28 pixel format. Here’s a breakdown of how CNNs work for digit recognition:
- Architecture of CNN for Digit Recognition
- Input Layer: Takes in the image, usually preprocessed to grayscale (28x28 pixels for MNIST).
- Convolutional Layers: Apply convolution filters to extract features such as edges, shapes, and textures. Each filter detects a specific pattern, building from simple to complex features as layers go deeper.
- Pooling Layers: Reduce the spatial size of the representation, preserving important features while reducing computation. Max pooling is commonly used to retain the most significant features.
- Fully Connected (Dense) Layers: After convolution and pooling, the output is flattened and fed into dense layers, where the network learns to map the extracted features to specific digit labels (0-9).
- Output Layer: A softmax layer with 10 nodes (one for each digit) is used to produce probabilities for each digit class.
- Training Process
- Backpropagation and Optimization: During training, the network uses backpropagation and optimizers (like SGD, Adam) to adjust weights and minimize error, iteratively improving its accuracy in digit recognition.
- Loss Function: Cross-entropy loss is commonly used to measure the difference between predicted probabilities and actual labels, especially for classification tasks like this.
- Popular CNN Models for Handwritten Digit Recognition
- LeNet-5: One of the earliest CNN models, designed specifically for handwritten character recognition. It has a relatively simple architecture with just a few convolutional and pooling layers, making it efficient for smaller datasets like MNIST.
- Custom CNN Models: Many researchers and practitioners design small, custom CNNs with fewer layers (2-4 convolutional layers) for digit recognition tasks, as large models aren’t needed for the relatively simple task of digit classification.
- Performance on MNIST Dataset
- CNNs can achieve over 99% accuracy on the MNIST dataset due to their capacity to learn spatial hierarchies in digit shapes.
- Simpler neural networks, like feedforward networks, can also classify MNIST digits but usually require more neurons and are less efficient than CNNs, as they don’t leverage spatial information as effectively.
Additional Insights
-
Why CNNs Outperform Fully Connected Networks for Images:
- Parameter Efficiency: Unlike fully connected networks, CNNs drastically reduce the number of parameters by using local connections (filters) that detect features at specific locations in the image. This is essential for small datasets like MNIST, as fewer parameters mean lower risk of overfitting.
- Translation Invariance: Pooling layers (like max pooling) make CNNs more robust to shifts or variations in the position of features, allowing them to generalize better on handwritten digits, which can vary in alignment and size.
-
Further Optimizations in CNN Models for FPGA Implementations:
- Quantization and Fixed-Point Arithmetic: FPGAs can benefit significantly from weight quantization, where weights are represented as fixed-point numbers rather than floating-point. This conserves memory and power, making it ideal for real-time applications.
- Hardware-Friendly Architectures: Reducing model depth and using shared filters can make CNNs more hardware efficient on FPGAs, especially with 784 weights, as you mentioned earlier, optimizing memory usage and processing speed.
-
Advanced Techniques for Robustness and Accuracy:
- Data Augmentation: Techniques like rotation, scaling, and random translation can create variations in training data, helping the model generalize to real-world variations in handwriting.
- Dropout and Batch Normalization: These regularization techniques help improve CNN performance by preventing overfitting and improving training stability, though they require careful adaptation for efficient FPGA implementation.
-
Comparative Alternatives in Architecture for Image Tasks:
- Capsule Networks: Unlike CNNs, capsule networks aim to capture spatial hierarchies between features directly, potentially making them more effective for complex images or variations in handwriting. However, they are more computationally intensive and less popular for MNIST-scale tasks.
- SqueezeNet and MobileNet: These CNN architectures, designed for efficiency, use bottleneck layers and depthwise separable convolutions, which are memory-efficient. They might be considered for large-scale image processing on FPGAs but are generally unnecessary for MNIST.
By using CNNs, particularly with optimizations for FPGA, we leverage both accuracy and efficiency for handwritten digit recognition, making them a powerful choice for real-time, resource-constrained applications.
Training for obtaining Weights and Biases
In a CNN trained on the MNIST dataset, weights and biases are obtained through a process called training, which involves iterative adjustments to minimize the error between the network's predictions and the actual digit labels in the dataset. Here’s a breakdown of how this happens:
1. Initialize Weights and Biases
- Random Initialization: At the start of training, weights and biases are typically initialized randomly. This initial randomness helps prevent the network from being biased toward any particular pattern in the beginning, allowing it to learn from the data.
- The initialization strategy (e.g., Xavier or He initialization) can help ensure that weights start with appropriate values, preventing issues like vanishing or exploding gradients.
2. Forward Propagation
- During forward propagation, each layer in the CNN processes the input data, using convolution operations in the convolutional layers and dot products in the fully connected layers.

- The activation function (like ReLU or sigmoid) is then applied to z to produce the neuron’s output.
- This process is repeated across layers, finally producing probabilities for each digit class (0-9) in the output layer using softmax activation.
3. Compute Loss
- Cross-Entropy Loss is the common loss function for classification tasks. For each image in the MNIST dataset, the loss is calculated based on the difference between the predicted probabilities and the true digit label.
- For example, if the correct label is "5" but the model predicts "3" with higher probability, the cross-entropy loss quantifies this error.
- The goal of training is to minimize the cross-entropy loss across all images in the training set.
4. Backpropagation
- Backpropagation is the process of calculating how much each weight and bias contributed to the error in the network’s prediction.
- This involves the chain rule of calculus, which allows the model to compute partial derivatives of the loss with respect to each weight and bias.

5. Weight and Bias Update (Gradient Descent)
- Using an optimization algorithm like Stochastic Gradient Descent (SGD) or Adam, the weights and biases are updated in the direction that reduces the error.

- This process is repeated for each weight and bias in the network, adjusting them to reduce the loss.
6. Iteration Over Epochs
- This forward and backward pass through the entire training dataset constitutes an epoch.
- Typically, CNNs are trained over multiple epochs to allow the weights and biases to gradually converge to values that minimize the loss.
- After each epoch, the network’s performance on the training and validation datasets is evaluated, which helps monitor the progress and detect issues like overfitting.
7. Convergence
- As training progresses, the adjustments to weights and biases become smaller, indicating convergence toward optimal values that minimize the error.
- Once the loss reaches a stable low value or other stopping criteria are met (e.g., a maximum number of epochs), the training process ends.
- The final set of weights and biases represent the trained CNN, which should now be able to accurately recognize handwritten digits on new, unseen data.
Neural Network Architecture
Architecture for the feedforward fully connected neural network for MNIST digit recognition, with the output handled by a max finder unit instead of a Softmax activation.
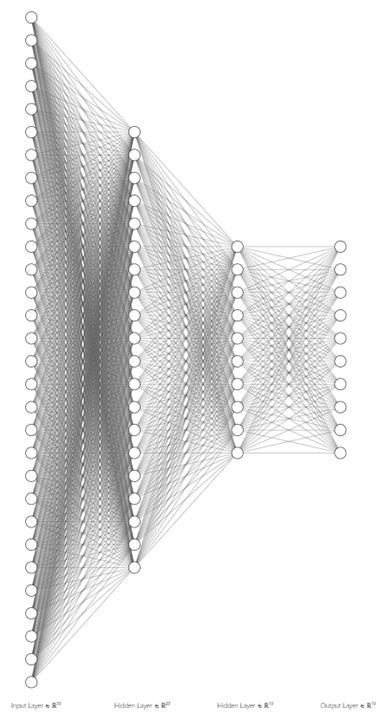
Network Architecture
-
Input Layer:
- The MNIST dataset images are 28x28 pixels, yielding 784 pixel values.
- The image is flattened into a 1D vector of 784 values, passed to the first hidden layer without any neurons in the input layer itself.
-
Hidden Layer 1:
- Configurable number of neurons (e.g., initially set to 30).
- Each neuron is fully connected to the 784 pixel values from the input layer.
- Activation Function: Set to either ReLU or Sigmoid via a switch, allowing flexibility.
-
Hidden Layer 2:
- Configurable neuron count (e.g., 30).
- Fully connected to all neurons from the previous layer.
- Activation Function: Controlled by a switch to either ReLU or Sigmoid.
-
Hidden Layer 3:
- Configurable neuron count (e.g., 10).
- Fully connected to neurons from Hidden Layer 2.
- Activation Function: ReLU or Sigmoid, depending on the switch setting.
-
Hidden Layer 4:
- Another layer with configurable neurons (e.g., 10).
- Fully connected to neurons from the previous layer.
- Activation Function: ReLU or Sigmoid, as specified by the switch.
-
Output Layer and Max Finder Unit:
- The final layer outputs 10 values corresponding to the 10 possible digit classes (0–9).
- Instead of using Softmax, a max finder unit compares the output values from each neuron in this layer. The neuron with the highest output represents the predicted digit, providing the final classification directly.
Summary of Architecture
- Input Layer: Passes 784 pixel values.
- Hidden Layers: 4 layers with configurable neuron counts and ReLU or Sigmoid activation (determined by a switch).
- Output Layer: 10 neurons, with a max finder unit that identifies the neuron with the highest output as the predicted digit.
This architecture avoids Softmax in the output layer, leveraging a max finder unit to simplify computation and reduce processing overhead, making it efficient for hardware implementation, such as on FPGAs.
