Blog #3: CNN HW Accelerator for Handwriting Recognition - Defining the Neuron for Handwritten Digit Recognition

Defining the Neuron

Weighted Sum and Bias

For a neuron in a given layer, the output before activation (also known as the pre-activation value) is calculated as follows:

Activation Function Application

After computing the weighted sum z, the neuron applies an activation function (e.g., ReLU, Sigmoid) to introduce non-linearity.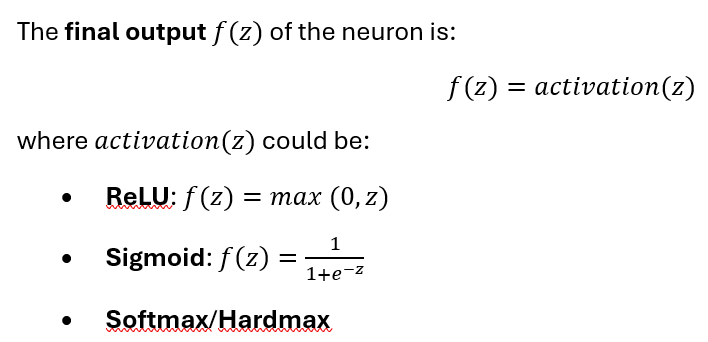

In a neural network, this process repeats across all neurons in each layer, allowing the network to learn complex patterns by adjusting weights and biases during training through backpropagation.

Types of Activation for Handwritten Digit Recognition in CNNs

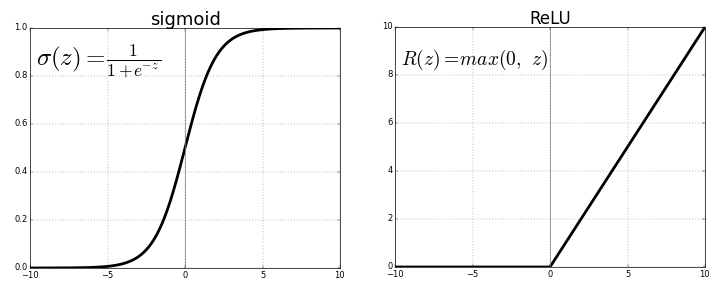
For a CNN designed to recognize handwritten digits, three types of neurons can be applied in different layers of the network: ReLU, Sigmoid, and Softmax/Hardmax. Each has unique properties that can contribute to different parts of the network:

1. ReLU (Rectified Linear Unit) Activation
   • Purpose: ReLU introduces non-linearity, enabling the network to capture complex relationships in the data by allowing it to learn non-linear mappings from input to output.
   • How It Works: The ReLU activation function outputs the input directly if it’s positive; otherwise, it outputs zero. This simple operation introduces non-linearity, helping the network model complex relationships in the data.
   • 
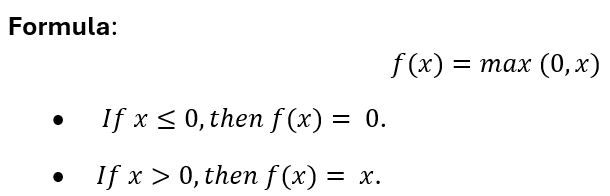
   • Example: For an input of , ReLU outputs 0, and for , ReLU outputs 2.
   • Advantages: ReLU neurons reduce the likelihood of vanishing gradients and are computationally efficient, making training faster and more stable in deep networks.
   • Where Used: Generally used after each convolutional and dense layer to create a rich feature hierarchy for digit patterns.
     
2. Sigmoid Activation
   • Purpose: The Sigmoid function, which maps input values to a range between 0 and 1, can be useful in networks where probabilities are important or where binary classifications or gating functions are involved.
   • How It Works: The Sigmoid function maps any input to a value between 0 and 1, making it suitable for binary classifications or when probabilities are needed. It compresses large positive or negative values towards 1 or 0, respectively.
   • 
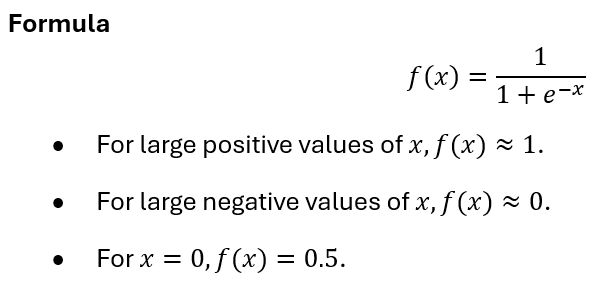
   • Advantages: Sigmoid activations can be beneficial in shallow networks and some specialized cases where output values between 0 and 1 are needed.
   • Disadvantages: Sigmoid neurons can suffer from vanishing gradients, especially in deeper networks, making them less common in CNNs with several layers.
   • Where It Might Be Used: Sigmoid is rarely used in hidden layers of a CNN for digit recognition due to vanishing gradient issues, but it might occasionally be used for gating mechanisms or in very shallow networks.
3. Softmax Activation for Output Layer
   • Purpose: Softmax neurons convert the final layer’s outputs into probabilities, ideal for multi-class classification (digits 0-9).
   • How It Works: Softmax normalizes the output into a probability distribution, where the sum of all outputs equals 1, making it clear which class is most likely.
   • Advantages: It provides interpretable probability scores for each class, which is ideal for classification.
   • Where Used: Exclusively in the output layer of a digit recognition CNN, where it generates a probability for each digit class.
4. Hardmax Function
   • In Hardmax, only the highest value in the output vector is set to 1, and all other values are set to 0. This makes the output a binary vector with a single 1, representing the index of the most likely class, and 0s elsewhere.
   • 
   • 

5. We will prefer Hardmax due to resource constraints, determinism, and reduced latency and computation on the FPGA

Hardware Architecture

This diagram illustrates the architecture of a single neuron for an FPGA-based neural network. Here’s a step-by-step breakdown of its components and data flow:

1. AXI Lite Interface for Configuration:
   • An AXI Lite interface is used to load the weights and biases for each neuron. Through this interface, data (weights and biases) can be written directly to the neuron’s memory using configuration signals. This enables flexible and efficient loading and updating of weights and biases for each neuron in the network.
2. Neuron and Layer Identification:
   • The config_neuron_num and config_layer_num signals indicate the specific neuron and layer within the network, allowing each neuron to be uniquely addressed.
   • Comparators check if the incoming config_neuron_num and config_layer_num match the neuron’s own identifiers (Own Neuron Number and Own Layer Number). This ensures that weights and biases are only loaded into the correct neuron, maintaining separation between different neurons and layers in the network.
3. Weight and Bias Memories:
   • Weight Memory: This stores the weights (w) for each input. The weights can be preloaded using Memory Initialization Files (MIFs) or loaded via the AXI Lite interface.
   • Bias Memory: Similarly, biases (b) are stored here and loaded based on configuration matching, allowing unique biases for each neuron.
4. Data Buses for Weights and Biases:
   • Weight Data Bus and Bias Data Bus: These buses carry weight and bias data into the respective memories when weightValid and biasValid signals are asserted, indicating valid data for storage.
5. Input Processing:
   • The neuron input (x) arrives on the neuronInput signal and is processed with each weight. The Weight Address Counter increments with each new input, ensuring weights are accessed sequentially from memory.
   • The Input Element Counter tracks the position of each input element and validates each incoming input using the inputValid signal.
6. 7. Activation Function:

1. • The output z passes through an activation function. This design supports either:
     • Sigmoid (using a ROM lookup for efficiency), or
     • ReLU, depending on configuration.
   • The result of the activation function is then provided as neuronOutput.

Benefits of Using Signed Fixed-Point Representation with Configurable Data Width

• Efficiency: Fixed-point arithmetic is more resource-efficient than floating-point in FPGAs, allowing for parallel neuron implementations.
• Precision Control: By adjusting the integer and fractional bits at compile time, you can tailor the design to your network’s precision needs. Higher fractional bits increase precision, while higher integer bits extend the range.

Example of signed multiplication used inside the neuron

Signed-Fixed point representation is used to represent the weights and biases of the neuron. Parameters such as integer/fraction width for the weight, data width for neuron input and output, type of activation function to use (ReLU or Sigmoid) are configurable. This gives us the ability to customize the neuron according to our implementation strategy based on the resources available on the FPGA platform.

Let’s take data width as 8-bits (input, weights, output), with 784 weights in first layer neuron. Activation function is Sigmoid which will use the LUT ROM. Given below is the utilization for a single neuron on a Zynq-7000 SoC

The utilization report helps us to architect the neural network for the target. For instance, if the total number of neurons in our network is around ~70, then utilization for neurons comes to around 8%, leaving us plenty of resources unused. We can make use of these additional resources to increase the data width, thereby increasing the fractional part of the weight. This might increase the accuracy of our calculations which will improve the accuracy of the model overall.

Verification of the Neuron

The input test data (Grayscale image (28px  28px), 8-bits) is stored in a txt file. The weights are represented in 8-bit binary signed fixed-point notation and are read from a MIF file and stored as floating-point values in another text file. Then both files are read, and the input is multiplied and accumulated. Then the Python script prints the final sum before and after adding the bias.

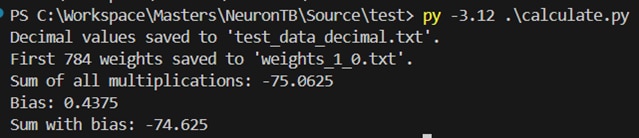
Now, a SystemVerilog test bench instantiates the neuron and feeds the input from the same TXT file one after the other into it. In the end, the test bench prints the sum calculated by the neuron in binary.

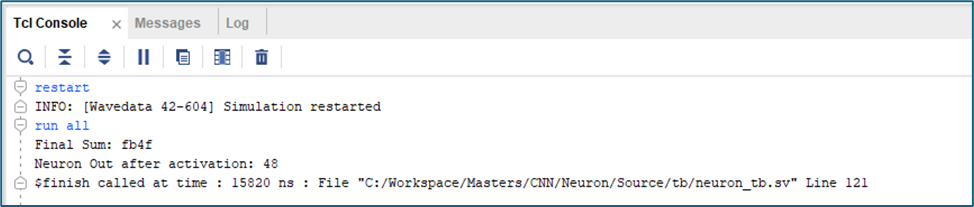
Hence, the result seems accurate given the resolution of the weights we had considered.

The bias will be added to the sum and then it will be fed into the respective activation function – which can be ReLU or Sigmoid, based on what’s specified in the neuron itself.

Source files, test bench, and the Python script used can be found here.

Thakns for reading!