In this post, I will talk about some of the relevant features of the firmware I am developing.

Reading ball height

I explained how to measure the distance between the ball and the SwishMaster in a previous post. Basically, I am leveraging the TDK USSM Arduino Library and, in particular, the GetDistanceCm() function.

Computing the ball trajectory

The main task of the firmware is to reconstruct the ball trajectory from the ball height readings. The process involves the following steps

• Get an approximation of the horizontal coordinate. USSM does not provide a reading for the horizontal position of the object -just the time of flight of reflected sound waves
• Correct measurement depending on horizontal position. Given the estimated horizontal position, the real distance between the ball and the sensor (i.e the distance measured along the sensor axis) can be calculated
• Align the axes: sensors measure distances in two different reference systems, which have to be aligned to make all the readings refer to a common reference system
• Compute the parameters of the parabola that best matches the points
• Compute the ball entry angle

1. Estimate ball horizontal position

As the basketball travels across the area covered by the USSM, we need to correct the measured distance to take into account the horizontal offset of the actual position of the ball from the sensor vertical axis. The sensor does not provide such an information, but it’s possible to estimate the ball horizontal position under the following conditions

• The ball speed is constant
• The ball distances are read at a fixed rate

In this scenario, the following algorithm works with a good precision

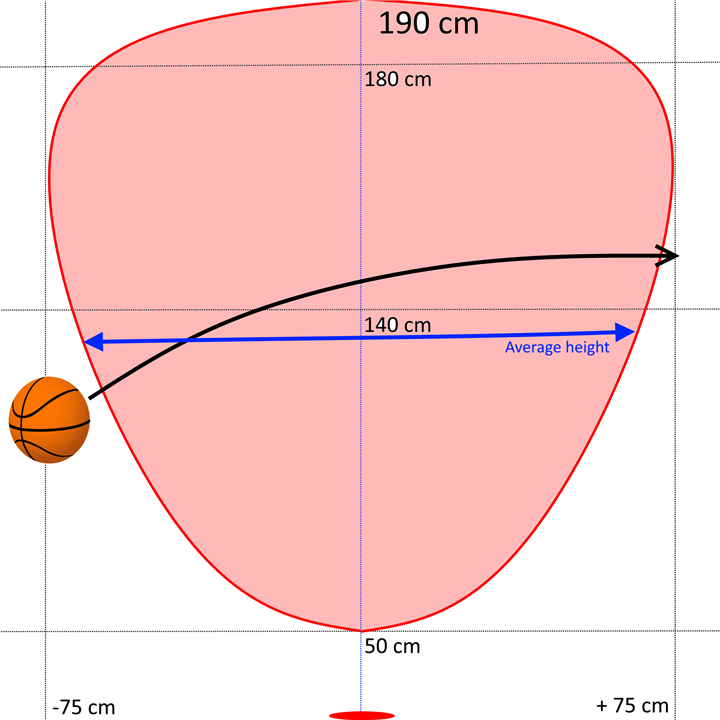
• Compute the average height of the ball
• Calculate the width of the covered area at the computed height
• The horizontal distance between samples is given by the area width divided by the number of sample

The area where the sensor can detect the basketball is approximated by a six-edges polygon, shown in the following picture

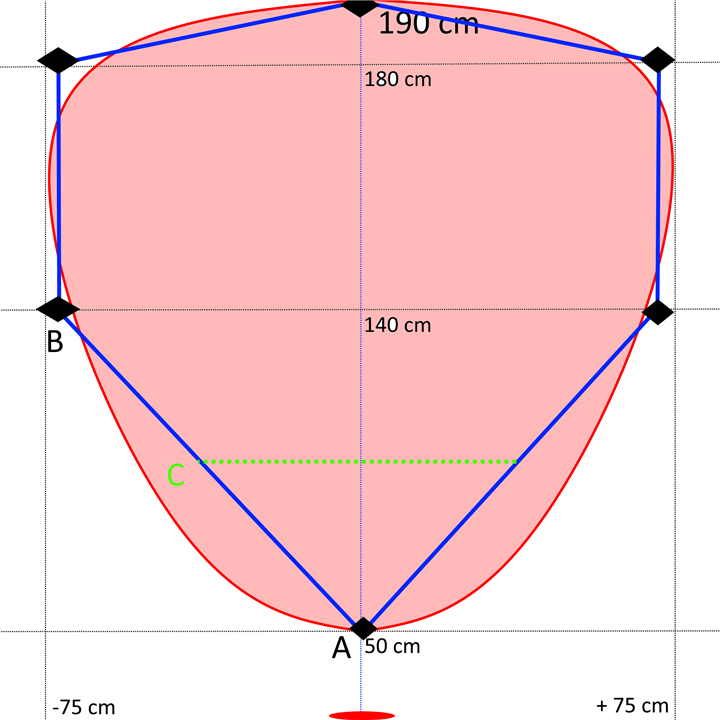
For example, the formula to compute the width of the covered area at a given height “C” is

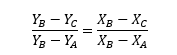
Where “Y” is the measured distance, and X is the width of the covered area. Solving the equation, we get

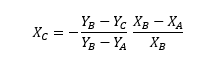
2. Correct measurements for horizontal position

Given the estimation of the horizontal position and the distance returned by the USSM, we can calculate the distance along the sensor axis using the Pitagora theorem

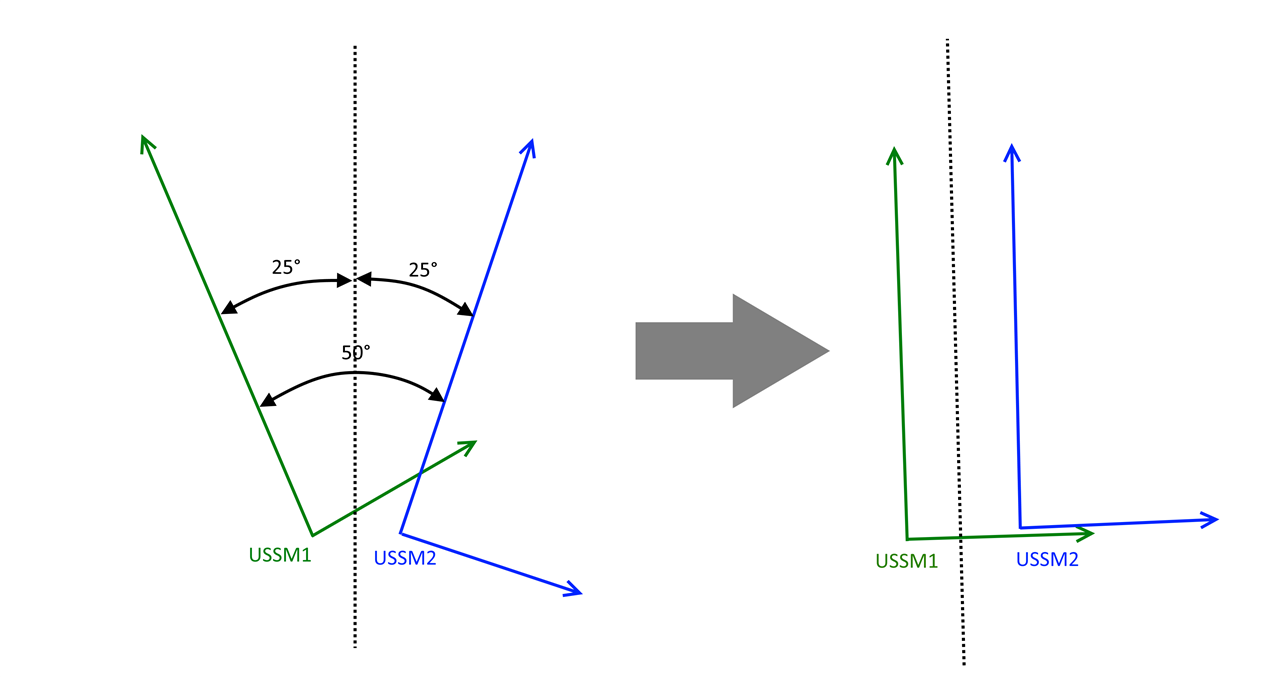
3. Aligning the axis

Samples are taken in two different reference systems, whose axis are 50 degrees apart. To align the axis, we need to rotate the axis 25 degrees clockwise and 25 degrees counterclockwise, as shown in the following picture

To rotate a point (x, y) around the origin by an angle θ (in degrees), the standard 2D rotation formulas are:

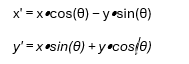
Finally, a translation is applied to make the origins overlap

4. Parabola fitting

This is essentially performing a quadratic regression to find coefficients a,b,c for:

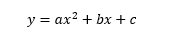
Using the least squares method for n points, the system of equations to solve is:

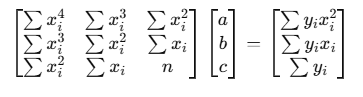
This 3×3 system can be solved using Cramer's rule. 

Cramer's Rule says that we can find the value of a given variable by dividing that variable's determinant by the regular coefficient-determinant's value. That is, Cramer's Rule specifies this relationship:

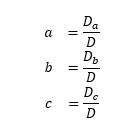
where D is the matrix determinant and Da Db, Dc are the matrix where the 1st, 2nd and 3rd columns have been replaced by the determinant D. Showing the C code is probably simpler than explaining the Cramer’s rule…

Parabola SwishMasterParabola::fit()
{
  // Summations
  double Sx=0, Sx2=0, Sx3=0, Sx4=0;
  double Sy=0, Sxy=0, Sx2y=0;

  for (int i=0; i<n; i++) {
    double xi = x[i];
    double yi = y[i];
    double xi2 = xi*xi;

    Sx += xi;
    Sx2 += xi2;
    Sx3 += xi2*xi;
    Sx4 += xi2*xi2;
    Sy += yi;
    Sxy += xi*yi;
    Sx2y += xi2*yi;
  }

  // Build matrices for solving
  double denom = (Sx4*(Sx2*n - Sx*Sx)
    - Sx3*(Sx3*n - Sx*Sx2)
    + Sx2*(Sx3*Sx - Sx2*Sx2));

  double a = ( (Sx2y*(Sx2*n - Sx*Sx))
    - (Sxy*(Sx3*n - Sx*Sx2))
    + (Sy*(Sx3*Sx - Sx2*Sx2)) ) / denom;

  double b = ( (Sx4*(Sxy*n - Sy*Sx))
    - (Sx3*(Sx2y*n - Sy*Sx2))
    + (Sx2*(Sx2y*Sx - Sxy*Sx2)) ) / denom;

  double c = ( (Sx4*(Sx2*Sy - Sx*Sxy))
    - (Sx3*(Sx3*Sy - Sx2*Sxy))
    + (Sx2*(Sx3*Sx2y - Sx2*Sx2y)) ) / denom;

  Parabola p = { (float)a, (float)b, (float)c };
  Serial.print("Parabola parameters: ");
  Serial.print(a);
  Serial.print(", ");
  Serial.print(b);
  Serial.print(", ");
  Serial.println(c);

  return p;
}

5. Ball entry angle

We have the fitted parabola

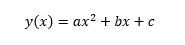
The slope of the tangent at any point x_0is simply the derivative:

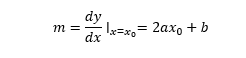
The angle with the horizontal is:

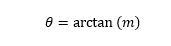
I just need to apply to formula to the last known point to get an estimate of the ball entry angle

And luckily...that's all

Sorry for the boring post full of formulas, but I think that some knowledge about the algorithm I implemented to computed the ball trajectory can make clearer how SwishMaster works. Next posts will focus on the case, the electronics and hopefully the first field test