I can't believe it's already week 4 of the challenge, but here we are. Michael Kellett's comments on my last blog post prompted me to do some calculations on the dimensions of my initial design. As such I have put off Matlab and actually 3D printing the mount until I am sure about the dimensions, material, structure, etc. I am going to use. I definitely welcome all comments and criticism on my blog as this is a learning experience for me too (I obviously don't design microphones for a living).
I was initially confused about the typical dimensions of condenser microphones, because I couldn't find a real explanation besides the usual: a larger diaphragm will have a bad high frequency response. But why is this exactly? And what is considered large?
If we are talking about vibrations in a membrane, most texts start with a description of the movement and various modes in a stretched rectangular membrane and then move on to variations where the membrane is circular, fixed at a rim and the vibrations are forced. The condenser microphone and the microphone I am designing are special cases of a fixed circular membrane with forced vibrations.
Basically you take a thin piece of material (thin means the thickness is much less than the other dimensions of the membrane, otherwise it's considered a plate) and stretch it to a certain tension which is lower than the maximum allowed tension. Now it is quite obvious that the tension of the material will determine how much the membrane is displaced if a certain force is applied. The tighter the material is stretched, the less the displacement will be. But there is another important factor which is partially determined by the tension: the resonant frequency of the membrane.
Vibrations in a membrane can be described using the 2D wave equation. I will not go into this in detail, but the solutions of the 2D wave equation determine what the response of the membrane will be to an applied wave with a certain frequency and amplitude.
The first resonant frequency appears at 
, since this is the first zero of the Bessel function 
(you can calculate all zeros at http://keisan.casio.com/exec/system/1180573472) . 
is the wave number and 
is the diameter of the membrane (a list of symbols is given at the end of this blog post).
The fundamental frequency for a circular plate fixed at the rim is:
Where 
is the surface density of the membrane in kg/m² and 
is the tension applied to the membrane in N/m.
As an example we can calculate the resonant frequency of a circular membrane with a diameter of 
, made of 
aluminum foil. Aluminum has a density of 
.
To start our calculations we first need to determine how much the foil will be stretched. I'm not quite sure how I will measure this in practice, but suppose the maximum allowed tension is 
(this will actually depend on the membrane thickness and the maximum allowable stress).
The surface density of the membrane is calculated by multiplying the density by the thickness of the membrane:
As stated earlier, the fundamental frequency appears at 
. And for a uniform circular membrane we can calculate the value by:
Not very good for a general purpose microphone right? However, keep in mind that a practical microphone will have some form of damping, which will decrease the peak at resonance, somewhat extending the usable range. However, it will still be way below the audible range.
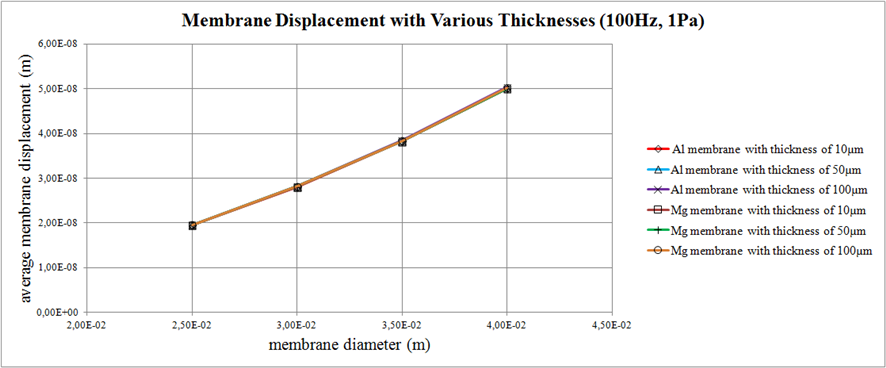
So how can we increase this? Well the first thing we could do is to try and increase the tension of the membrane, however this will decrease the average displacement as we will see next. The other thing we can try is to decrease the diameter, but this will again decrease the displacement of the membrane (which is more effective?) Finally, we could try using another material, preferably one with a lower density as you can clearly see from the formula. Copper and Steel both have a much higher density than aluminum as do most metals (which is intuitive because aluminum is pretty light). The only other candidate I can think of that has a decent permeability (if we are thinking ahead, for the LDC1000's requirements) is Magnesium, which has a density of only 1700kg/m^3.
The following figure shows the influence of various design parameters on the basic fundamental frequency of the vibrating membrane.
The next important parameter is the sensitivity of the microphone. This will be determined by the resolution of the LDC1000 and coil, but also by the displacement of the membrane.
To determine the displacement we have to make certain assumptions. First of all the displacement will, over a large frequency range, depend on the frequency and the amplitude of the applied pressure wave. Second, we can determine either the displacement in the center, or probably more important in our case, the average displacement over the entire membrane.
from the center is:
Using the same values as before, we have:
The Bessel functions are:
The average displacement then becomes:
The next figure shows the influence of the membrane diameter, thickness and material on the average displacement.
The next figure shows the displacement at 100Hz, much lower than the resonance frequency:
is the resistivity of the metal, about 
for Aluminum.
and 
are the relative and absolute permeability which is approximately 
for Aluminum. At the maximum frequency of 5MHz we get:
