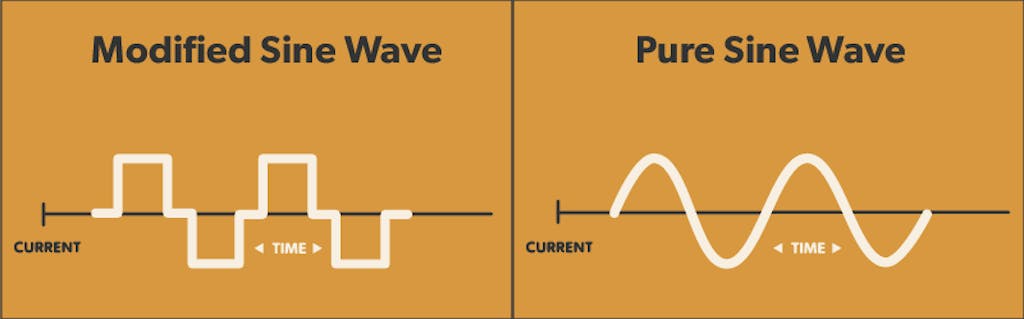
I'd like to see a Design Challenge for a sine wave or modified sine wave inverter at perhaps 100 watts, with a 12 or 24 VDC input, 120 VAC or 240 VAC, and 50 or 60 Hz Output. It's a lot easier to design a modified-sine wave inverter (also called quasi-sine) than a true sine wave inverter. The modified sine wave inverters have a square waveform with a large dead band at the edges like the image below on the left.
Back to the design. The two main topologies are single-stage switching where the DC input is switched by an H-Bridge that feeds a low-frequency (power-line frequency) transformer that both isolates and steps-up the voltage to 120 VAC or 240 VAC. The other method uses two stages where the first stage is a step-up DC-DC Converter with a 200 or 400 VDC output (200 VDC for 120 VAC and 400 VDC for 240 VAC out) which gets followed by an H-Bridge inverter to provide the 50 Hz or 60 Hz sine wave output. With the proper control method, the RMS AC output voltage can be adjusted or regulated. In the case of the modified-sine output, the AC output gets increased by making the pulses wider and it gets lowered by narrowing the pulses. In this type of inverter, no LC output filter is typically used, except possibly for EMI reduction purposes. In the two-stage inverter, the pulses are rectangular and the output gets converted to a sine wave by the low-pass smoothing filter. A simplified schematic of both the single and two-stage inverters can be seen below.
These two topologies can also be used to make either a modified sine wave or a true sine wave output. For a true sine wave output, this is accomplished by Pulse Width Modulation (PWM). The diagram below shows how this is done. One only has to consider one half of the waveform, so let's consider the positive half cycle since the negative half is exactly the same, except inverted with respect to the 0 (zero) VAC line across the center going from left to right. There's actually no line going across in the picture, so please use your imagination for the zero line, about half way between the top and the bottom of the diagram. The way it works is, with the sine wave starting at zero and rising, the control circuitry produces rectangular pulses of a width proportional to the amplitude value of the sine wave each point where a rectangular pulse starts. Typically, many more pulses are used in a full sine cycle than are shown (typically from 16 to 64 or more), but it's easier to see the principal with just a few pulses. As the sine wave increases, so does the width of the rectangular pulses and the pulse width continues to increase until the peak of the sine wave is reached for which the pulse will have the maximum pulse width. Notice in the diagram that when the sine wave has peaked, the pulse width has also peaked and as the sine wave comes back down toward zero on the second half of the positive half cycle (2nd quarter sine cycle), the pulses become narrower till they reach a minimum or zero width at the sine wave's zero crossing. The process repeats for the sine wave's negative half-cycle except that the H-Bridge inverts the pulses polarity to be negative with respect to the center zero voltage line..



Now, I admit that these pulses do not look like a sine wave; however, they contain the sine information in their pulse width. So all we need to do is decode this somehow and this is done using a low-pass LC filter, which averages the effective DC value out of each pulse, albeit with a bit of superimposed ripple on the recovered sine wave. In order to get good sine wave purity, we need to filter the pulse train well. A good pulse switching frequency for power inverters is 20 KHz, which cannot normally be heard by the human ear. Although the switching frequency can certainly be higher and up to 100 KHz or even more, the switching losses become too high above 20 KHz, so most inverters use 20 KHz or less for a switching frequency. Since the output sine wave is at 60 Hz (or 50 Hz), it's about 2.52 decades away from the 20 KHz switching frequency. We must select a center frequency for the LC filter that isn't so close to the 50/60 Hz output frequency that it starts to attenuate it, nor should it be too close to the switching frequency or else the attenuation of of the switching pulses will be too small causing the switching ripple on the sine wave output to be too high. A good trade-off is a decade above the output frequency or 600 Hz. At 60 Hz, the filter's cutoff frequency will be: log(20,000/600) = 1.523 decades away from the 60 Hz output. A two pole filter yields 20 dB/Decade/pole * 2 poles = 40 dB/Decade attenuation. The total attenuation of the switching pulses in this case will be 40 dB/dec * 1.523 = 60.9 dB. This corresponds to an attenuation ratio of: 10^(60.9/20) = 1,111. Therefore, at 120 VAC RMS output, the switching ripple will be approximately: 120V*SQRT(2)/1,111 = 153 mV, which is not bad and it equates to about 0.13% output ripple. For inverter switching, MOSFETs work well, although one certainly could use bipolar transistors, IGBTs, or GaN FETs.
Here's a photo of a 2,500 watt, 24 VDC to 120 VAC, Sine Wave Inverter I designed, with the top cover removed. The adjacent photo shows the Inverter's Digital Control Board along side of one of it's two MOSFET Half-Bridge Power Boards. Each Power Board is a Half-Bridge containing 32, TO-220 MOSFETs (2X16 in Parallel) switching at 20 KHz. There are two large electrolytic caps plus a few smaller film caps across the 24 VDC supply to minimize supply voltage spikes due to switching. The Power Board also has a Current Transformer to measure the Primary Current in the Power Transformer (not shown). The Control Board on the left has a 176-Pin LQFP Package IC and is a TI, C2000 Series DSP (TMS320F2812). All the control functions are run by custom C-Code that was compiled and downloaded to the DSP chip using the TI Code Composer Studio (CCS) software tools. The Control Board has 10 LEDs in the upper-right and 9 switches which are for status and inverter testing respectively. The inverter shown has a single-stage with a 60 Hz power transformer. This 2,500 watt (continuous) inverter is capable of supporting output power surges of up to 10,000 watts for a few seconds for motor starting and other similar loads that need high current at startup.


Other parts of a complete inverter circuit that are needed are: housekeeping power supplies to run the control circuitry and Fet Drivers, and a means of getting a scaled-down version of the 120/240 VAC output to the control circuit for voltage feedback for regulation. This feedback can be done with a small isolation transformer, a linear opto-coupler circuit, or an isolation amplifier IC. Note that if an isolation amplifier is used, it also needs an isolated 5V supply referenced to the high-voltage side. As can be seen in the photo of the 2500 watt inverter, the power transformer is in the center with the white wrapper and is quite large, as the transformer runs at a power-line frequency of 50 or 60 Hz. This single-stage inverter has a large size and weight and those are it's main disadvantages. It's main advantages are it's simplicity, ruggedness, and robustness. With the two-stage inverter, it's more complicated as it has two separate switching stages, but it has the advantage of not needing a large, 50/60 Hz transformer. Instead, it uses a small, high-frequency DC-DC Converter, and its transformer's size and weight will be much less.
That's all for this blog. I'll likely be posting additional blogs on Power Electronics, specifically, DC-DC Converters, DC-AC Inverters, AC-AC Frequency Converters, and AC-DC Power Supplies including Power Factor Correctors.
