Designing Low-cost, Multiple Output DC-DC Converters
Using 1:1 Coupled Inductors with Buck Regulators
1. Introduction
Power supply circuitry is always limited by cost, PCB area, height and by the desire to reduce complexity. The majority of systems today are mixed-signal, and in all but the simplest cases, the various analog and digital circuits need several different supply voltages to operate. One way to add additional outputs to a power supply without adding additional control ICs is to replace the standard inductor of a buck regulator with a multi-winding inductor. One winding is energized by the buck regulator, and there are many ways to create a second output by rectifying and filtering the voltage induced in the second winding. Buck regulators are found in nearly every power supply architecture, and the multi-winding inductor can be custom-wound to provide various turns ratios and even multiple outputs, but in the interest of controlling both complexity and cost, this application note will focus on off-the-shelf, 1:1 coupled inductors. Würth Elektronik eiSos offers several families of 1:1 coupled inductors with varying power levels and pinouts, many of which are suitable for adding a secondary output to a buck regulator.
2. The Three Most Common Used Topologies
Figures 1a, 1b and 1c show the three topologies that are most often used. Figure 1a shows how the secondary voltage, VOUT2 can be stacked on the main output voltage, VOUT1, creating a total voltage with respect to system ground of (2 x VOUT1). Figure 1b shows how the return of the secondary output can be connected to the common of an isolated secondary, creating an isolated voltage that could be used to power sensors or isolated communications equipment. (Note: most 1:1 inductors are not rated to withstand the voltages in isolated AC mains or telecom circuits. Isolation with 1:1 inductors is used to insulate against electrical noise.) In this case, the average value of VOUT2 is equal to VOUT1. Figure 1c shows how the system ground can be shifted to the other side of the secondary output capacitor to create a negative voltage. In this case, the absolute value of VOUT2 is equal to VOUT1.
 | 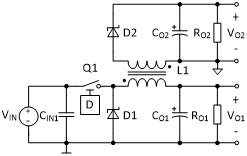 |  |
| Figure 1a: Stacked for 2x VOUT | Figure 1b: Isolated VOUT2 | Figure 1c: Negative VOUT2 |
In all three cases the control loop of the buck regulator only regulates VOUT1, and hence the actual value of VOUT2 will vary with input voltage, with the voltage drops across the output diode in the secondary, with the load currents in both the main output and the secondary output and with duty cycle. For this reason a linear regulator is often used on the secondary to provide a truly regulated secondary output voltage.
3. Design Example
The following equations and design philosophies will guide the user through the steps needed to add a secondary output to a non-synchronous buck regulator using a control IC with a fixed current limit. Most buck regulator ICs with internal power MOSFETs have a comparator that monitors the current flowing through the control or “high-side” MOSFET (Q1 in Figure 1), which is equal to the main inductor current when this MOSFET is on. Good quality ICs will specify a minimum threshold for this current limit over the full range of operating temperature, and in most cases when this limit is reached the IC will immediately turn the MOSFET off. As will be shown, this represents a maximum output power that must be shared between the main output and the secondary output. For the design example the IC used will be the TPS54160 from Texas Instruments. The Electrical Characteristics table of the datasheet states that the minimum current limit threshold over the full temperature range is 1,8A. The design specifications are as follows:
The selection of the external components is the same regardless of how the secondary is connected; hence these calculations are valid for the cases shown in Figure 1a, 1b and 1c.
4. The 1:1 Inductor
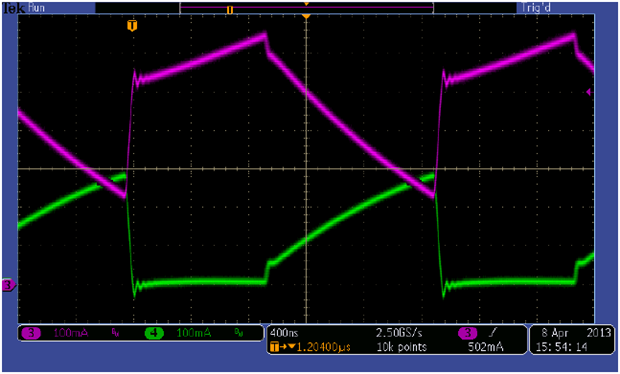
Magnetics form the heart of any switching converter, from this example delivering 3,5 W to a multiphase fullbridge converter delivering kilowatts of power. For the 1:1 coupled buck the principal difference from a standard buck is the increase in peak-to-peak ripple current induced in the main (primary) winding. This is due to the additional energy stored and delivered to the secondary output, and the induced current changes the waveshape from a triangle wave to a trapezoid wave. Figure 2 shows the currents in the primary winding in pink and the secondary winding in green. The dot convention of the two windings is arranged so that the secondary winding conducts while the control MOSFET is off and the recirculating diode (D1) is on. In this way the average voltage over a switching cycle applied to the secondary is approximately equal to VOUT1.
Figure 2: Primary (pink) and Secondary (green) Currents in the 1:1 Coupled Inductor
It is important to distinguish between the average current and the DC current for the secondary. “Average Current”, IS-AVG, refers to the average height of the trapezoid waveform. “DC Current”, IO2-MAX, refers to the average current delivered to the load on the secondary. These two currents are not the same value, and much confusion can result from mixing them up. For clarity, the Average Current of a trapezoid waveform is equal to the DC Current divided by one minus the duty cycle. For the case of the secondary in a 1:1 coupled buck the maximum values are of interest for worst case calculations:
VD1 is the typical forward voltage of the recirculating diode, D1
The inductance per winding is selected in the same way as with a standard buck, and is based upon the control of the peak-peak ripple current in the primary winding, denoted ∆pTRI:
5. Inductor Ripple Current
One of the most important decisions to be made in designing the converter is how much ripple to allow. In normal buck converters the peak-peak ripple is usually set at 20 % to 40 % of the maximum DC output current. The range of 20 % to 40 % represents a good compromise, tested and confirmed by the design of countless switching converters, and gives a balance between size (larger ripple requires less inductance and therefore smaller inductors) and efficiency/noise (smaller ripple leads to lower RMS currents and lower EMI).
EQ.4 selects the inductance for the purely triangular portion of the primary ripple current, but the total ripple current, ∆iP, is equal to the sums of primary triangular and the total secondary ripple currents. Due to this additional ripple, the recommended range for ∆iP-TRI is lower - from 10 % to 30 % of the maximum output current of the primary, IO1-MAX. For this example ∆iP-TRI = 30 % = 0,15 A:
The next highest standard value of inductance is 47 μH, and this value, denoted L1, will be used henceforth. The triangular portion of primary ripple current is then:
Calculating the ripple current in the secondary is unfortunately much less straightforward. This quantity is highly dependent upon the leakage inductance of the 1:1 inductor, the load current, the forward voltage drop of the output diode, and the DC resistance (DCR) of the inductor windings (Figure 3).
Figure 3: 1:1 Inductor with 1st Order Parasitic Components and Voltage Drops
Closer inspection, especially at higher secondary output currents reveals that ∆iS is not purely triangular, but is in fact a parabola due to the trapezoid waveform of the voltage applied across the leakage inductance. An approximate equation is given here, based upon the assumption that the average voltage across the leakage inductance is constant and is equal to the forward voltage of the output diode:
The difficulty in using this expression stems from accurately measuring the leakage inductance and from accurately predicting (or measuring) the diode voltage VDS. Leakage inductance is not always specified by inductor manufacturers, but it can be measured by short-circuiting one set of terminals of the inductor and measuring the inductance of the other terminals. For this example LLEAK was measured as 3,1 μH. Diode voltage must be assumed, hence a value of 0,5 V will be used.
Now that ∆iS has been estimated the total primary ripple current can be calculated:
Peak current can now be calculated for the primary:
Peak current can be calculated for secondary after the peak-peak secondary ripple current has been calculated:
The final step required before an actual inductor can be selected is to calculate the RMS currents for both the primary and the secondary. For the primary, using the DC output current is quick and very close to the true RMS value. For the secondary, the RMS value of a trapezoid wave is:
6. The Right Inductor
In conclusion, the desired inductor should have an inductance of 47 μH per winding, be able to support a peak current of 0,74 A without saturating, and able to carry RMS currents of 0,5 A in one winding and 0,32 A in the other without overheating. With 1:1 coupled inductors it is especially important to read the datasheets carefully and to understand the conditions under which the saturation and RMS current ratings are valid. Good quality manufacturers will state these conditions explicitly. The Würth Elektronik WE-DD series of coupled inductors includes the 744878470, whose electrical characteristics are repeated below:
Würth Elektronik Order Code | L (µH) | IR (A) | ISAT (A) | RDC-TYP (Ω) | Farnell Order Code |
| 744878470 | 47 | 0,9 | 1 | 0,6 | 1869658 |
IR 40ºK over ambient temperature when both windings in series are energized by rated current mentioned. ISAT inductance drop of 10% typical when one winding by saturation current mentioned.
The ISAT rating is for the combination of the currents in both windings, however one fortunate aspect of 1:1 coupled bucks is that when current in one winding is at its peak, current in the other winding is at its valley, and hence the primary peak current IP-PEAK represents the worst case.
7. Limits for Maximum Secondary Current
Two conditions limit the maximum current that the secondary output of a 1:1 coupled buck can deliver. The first is derived from the current limit threshold of the control IC. For this example where ILIM = 1,8 A:
This condition is most likely to occur when both outputs are delivering maximum load current and when input voltage is at a maximum.
The second limitation comes from the boundary between Continuous Conduction Mode (CCM), where the current in the primary winding never reaches zero, and Discontinuous Conduction Mode (DCM), where primary current falls to zero before the end of the switching cycle. This limitation applies to non-synchronous buck converters and some synchronous buck converters if their control ICs do not allow inductor current to reverse polarity. Once the converter enters DCM the average voltage across the primary winding is less than VOUT1. VOUT2 tends to droop or even collapse, depending upon the load current it supplies. For all switching regulators the CCM/DCM boundary can be defined as the point when average inductor current equals onehalf of the ripple current. Referring back to Figure 2, it is clear that this condition is most likely to occur when primary load current is low and secondary load current is high.
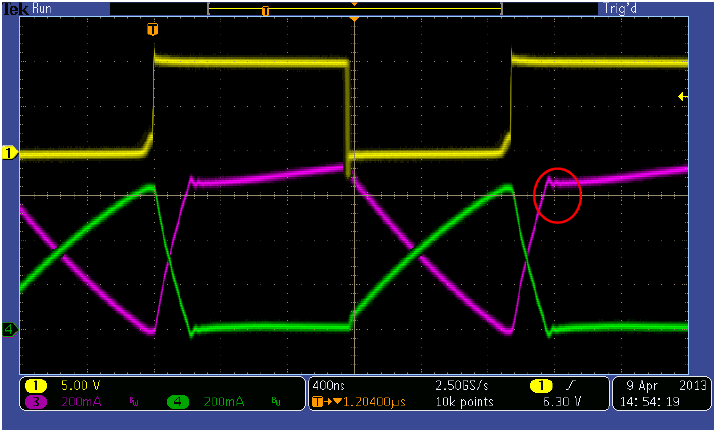
Writing a useful equation is difficult because of the high variability of the secondary ripple current and its dependence upon the non-linear relationship of the secondary output diode forward voltage to forward current. Lab testing is the best way to determine when the converter will enter DCM, and a current probe will show the exact point where primary current hits zero. If a current probe is not available, then a voltage probe and a multimeter will work. Figure 4 shows the switch-node voltage of the primary (where the control FET, inductor primary and diode all connect) just in DCM. The voltage probe will reveal the onset of a damped oscillation before the end of each switching cycle, and a multimeter will show the rapid drop in VO2 once DCM is reached.
Figure 4: Primary switch node voltage (yellow). The section circled in red indicates DCM.
If the desired secondary load current IO2-MAX is higher than the lower of these two limits, there are several remedies:
1. Current ripple can be reduced by increasing the inductance, increasing the switching frequency, or both. This helps with both types of limit.
2. For current limit: a different control IC with a higher current limit threshold or a controller with external power MOSFETs and an adjustable threshold can be used.
3. For DCM limit: switching to a synchronous buck regulator that allows current in the inductor to reverse polarity and flow below zero allows the converter to maintain an average voltage of VOUT1 across the windings of the 1:1 inductor even when IO1 = zero. Several semiconductor companies have released small, cost-effective synchronous buck regulators targeted towards this application.
There is also a minimum current that the secondary output must supply in order to prevent VOUT2 from increasing at light or no-load conditions. The cause of this increase is a gradual transfer of energy to the secondary output capacitors from the energy in the leakage inductance of the inductor. Measuring leakage inductance and attempting to calculate the minimum load is generally impractical, and for this example lab testing with a potentiometer proved quick and effective. To keep the absolute value of VOUT2 below 5,5 V a maximum resistance of 1,1 k is needed, and in the BOM a 1 k resistor is used.
8. Accuracy of the Secondary Output Voltage
One disadvantage of using coupled inductors to generate secondary outputs is that only the primary output voltage is regulated by the feedback loop. Depending upon the tolerance of the reference voltage and of the feedback divider resistors, the main output VOUT1 enjoys a typical tolerance of ±1% to ±4% of the average VOUT1 value. VOUT2 is unregulated, however, and will shift with changes in input voltage and duty cycle. VOUT2 shows a greater shift with respect to the load currents of both the primary and the secondary. This is due to the voltage drops across the diodes and across the DC resistance (DCR) of the inductor windings and the PCB traces. Figure 5 shows a 1:1 inductor treated as an ideal transformer with a coupling efficient of 1, driven by a voltage equal to VOUT1 on the primary. By reflecting the voltage drops from the primary to the secondary it can be seen that VOUT2 is directly proportional to IO1 and is inversely proportional to IO2.
Figure 5: Primary and secondary voltage drops affect VOUT2
The first-order equation governing VOUT2 is then:
In most design guides the forward voltage of a Schottky diode is assumed to be 0,5 V, however if VOUT2 is to be predicted with any accuracy the datasheets of the Schottkys used must be consulted or, better yet, the actual voltage drop measured. In practice the tolerance is also affected by the coupling coefficient between the two windings, and the effort of predicting VOUT2 to an accuracy of less than ±10 % is likely wasted, especially when the effect of load transients on either VOUT1 or VOUT2 are considered. For this example, even if the converter were sitting at just the right operating point to make the positive and negative terms of EQ.11 cancel, any load transient i would cause a shift of I * DCR. In conclusion, using VOUT2 without a linear regulator is only practical for loads that have few or no load transients and that can tolerate a fairly wide range.
Table 1 shows the tolerance of VOUT2 for this example over various load and line conditions:
Table 1: Secondary Voltage vs. Input Voltage, Primary Load and Secondary Load
9. Output Capacitors
Capacitors for smoothing the voltages at the converter outputs are selected with a similar philosophy as the inductor, but with a focus on maintaining a given maximum peak-to-peak ripple voltage instead of a ripple current. For the main output the ripple voltage is a function of the output capacitor´s impedance at the switching frequency and the peak-peak ripple current. The following equations assume that half of the impedance is due to the capacitive reactance, and half comes from the equivalent series resistance (ESR):
For this example, a solid tantalum capacitor with 220 μF and ESR of 40 m meets both requirements and provides much extra capacitance for responding to load transients. As a general practice, any time tantalum, aluminum or other high-ESR type capacitors are used at a switching converter´s input or output a 100 nF multi-layer ceramic capacitor (MLCC) placed in parallel will help reduce high frequency noise. The secondary output requires that CO2 both filter and hold up VOUT2 while the control FET is on. This requires both higher capacitance and a higher RMS current rating for an output of the same power. Fortunately VOUT2 only delivers a maximum of 200 mA. Minimum capacitance and maximum ESR are determined as follows:
Here it is important to calculate the RMS current as well:
Tantalum and aluminum capacitors are possibilities, but in the face of heavy RMS current, MLCCs are the best choice. For this example a 22 μF device rated at 10V with X5R dielectric and 1210 case size will be used. The ESR is approximately 3 m and the RMS current rating is about 3 A. One important consideration for MLCCs is their loss of capacitance under a DC voltage bias. This particular capacitor drops to about 16 μF when used at 5 VDC.
10. Input Capacitors
Input ripple voltage is often overlooked, but plays a vital role in conducted EMI. Input capacitors to buck regulators must withstand a discontinuous, heavy RMS current because they supply most of the AC current to the converter when the control FET is on. As with the secondary output capacitors, after minimum capacitance and maximum ESR have been selected, the capacitor or capacitors chosen must be evaluated for their RMS current ratings.
The RMS current through the input capacitor is calculated as:
MLCCs are again the best choice due to their low ESR and high RMS current ratings. Here, a 25 V rated 10 μF device with X5R dielectric will be used. When biased at 14 V, the actual capacitance is approximately 7 μF.
IMPORTANT NOTICE
Würth Elektronik eiSos GmbH & Co. KG and its subsidiaries and affiliates (WE) assume no liability for application assistance of any kind. Customers may use WE’s assistance and product recommendations for their applications and design. The responsibility for the applicability and use of WE Products in a particular customer design is always solely within the authority of the customer. Due to this fact it is up to the customer to evaluate, where appropriate to investigate and decide whether the device with the specific product characteristics described in the product specification is valid and suitable for the respective customer application or not. Customers are cautioned to verify that data sheets are current. The current data sheets can be downloaded at www.weonline. com. Customers shall strictly observe any product-specific notes, cautions and warnings. WE reserve the right to make corrections, modifications, enhancements, improvements, and other changes to its products and services. WE does not warrant or represent that any license, either express or implied, is granted under any patent right, copyright, mask work right, or other intellectual property right relating to any combination, machine, or process in which WE products or services are used. Information published by WE regarding third-party products or services does not constitute a license from WE to use such products or services or a warranty or endorsement thereof. WE products are not authorized for use in safety-critical applications (such as life support). It has to be clearly pointed out that the possibility of a malfunction of electronic components or failure before the end of the usual lifetime cannot be completely eliminated in the current state of the art, even if the products are operated within the range of the specifications. In certain customer applications requiring a very high level of safety and in which the malfunction or failure of an electronic component could endanger human life or health Customers must ensure that they have all necessary expertise in the safety and regulatory ramifications of their applications, and acknowledge and agree that they are solely responsible for all legal, regulatory and safety-related requirements concerning their products and any use of WE products in such safety-critical applications, notwithstanding any applications-related information or support that may be provided by WE. Further, Customers shall fully indemnify WE against any damages arising out of the use of WE products in such safety-critical applications. WE products are neither designed nor intended for use in automotive applications or environments unless the specific WE products are designated by WE as compliant with ISO/TS 16949 requirements. Customers acknowledge and agree that, if they use any non-designated products in automotive applications, WE will not be responsible for any failure to meet such requirements.
USEFUL LINKS
Application Notes:http://www.we-online.com/app-notes
Component Selector:http://www.we-online.com/component-selector
Toolbox:http://www.we-online.com/toolbox
Product Catalog:http://katalog.we-online.de/en/
DIRECT LINK
ANP017: Designing low-cost, multiple output DC/DC converters
CONTACTINFORMATION
Würth Elektronik eiSos GmbH & Co. KG
Max-Eyth-Str. 1, 74638 Waldenburg, Germany
Tel.: +49 (0) 7942 / 945 – 0
Email: appnotes@we-online.de











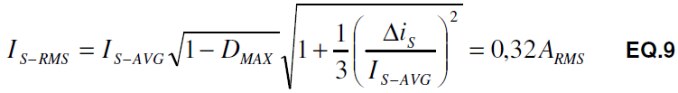
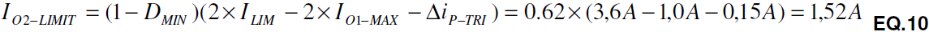





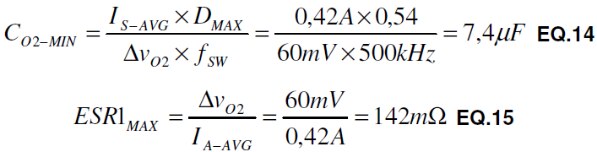
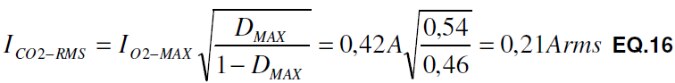
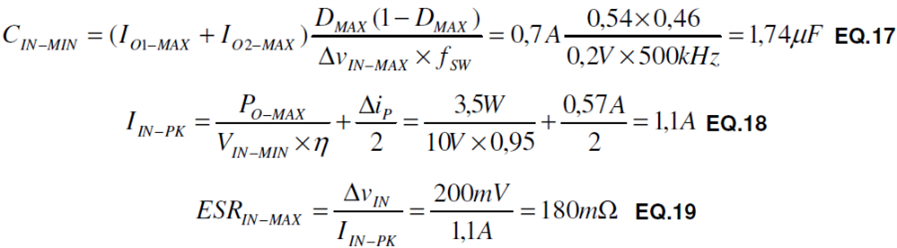

Top Comments