A Digital Signal Processor, commonly known as DSP, is a specialized microcomputer designed to process digital data that represents analog signals. DSPs are engineered to excel in high-speed numeric processing applications, making them indispensable in a wide variety of fields.
Related Components | Test Your Knowledge 

This Essentials course covers the basics of digital signal processing, including how to code common filters and the basic hardware components inside a DSP.
2. Basic Concepts
What will you learn about DSP?
- The difference between analog and digital signals
- How an analog signal is converted to digital
- What a digital filter is, and how to implement one
- The architecture of a DSP unit
- How to code a basic filter in both a high-level and low-level language
What’s the difference between Digital and Analog Signals?
To understand the workings of DSP, we first have to review the concepts of digital and analog signals.
Analog signals are continuous and represent quantities that vary smoothly over time and space. In the physical world, almost every signal is inherently analog; this includes sound waves, voltage levels, temperatures, brightness, and more.
Digital signals represent information using a finite set of distinct values, typically binary (0s and 1s). Digital signals are a result of the quantization and discretization of analog signals. Analog signals can be converted to digital and vice versa. One example of this is digital audio; music played back from a computer must be converted to analog format before we can listen to it. That’s not entirely true; if we attempted to listen to a digital signal, we might hear some screeching (though mostly out of our hearing range); however, we would not hear anything resembling music.
3. Analysis
What is DSP?
Digital Signal Processing (DSP) is a branch of engineering and mathematics that deals with the manipulation, analysis, and interpretation of digital signals. A Digital Signal Processor (DSP) is a processor or microcomputer that is optimized to execute the algorithms and arithmetic necessary for processing digital data that represents analog signals. This processing typically takes place in real-time. A series of individual samples arrives at the DSP from an analog-to-digital converter (ADC), and the DSP must complete all the calculations before the next sample arrives. In many cases, previous samples are updated as well.
Why use digital?
To dive deeper into the differences between digital and analog signal processing, let’s consider a bandpass filter. A bandpass filter removes any signal below and above certain frequencies. In the analog domain, this is accomplished with resistors, capacitors, and inductors. The circuit is relatively simple, but can be difficult to calibrate, especially if you want to customize the roll-off characteristics. If a steep roll-off is desired, fourth or fifth order filters may be required, with each stage potentially causing phase shift and changing the signal. In the digital domain, an ideal bandpass filter can be created with zero phase shift. Any modifications can be made by changing a line of software.
Figure 1 illustrates the output of an ideal bandpass filter compared to what you might get with a second-order analog filter. The ideal bandpass filter has a flat frequency response in the passband with zero phase shift and infinite attenuation in the stopband. The frequency response of the analog circuit is created by combining several staggered high-Q sections. Any adjustments to modify the roll-off characteristics or to obtain a flat frequency response would be very challenging.

Figure 1: An ideal bandpass filter and second-order approximations
In the DSP world, implementing a filter consists of simple arithmetic operations in great numbers. An ideal bandpass filter involves applying a transfer function with the appropriate coefficients to a large number of input samples (or taps, if you consider the train of input samples as a tapped delay line). Figure 2 compares the roll-off response of three analog circuits (2nd-order, 4th order, and 6th order Chebyshev filters) with a digital 90-tap FIR (Finite Impulse Response) filter.

Figure 2: 90-tap FIR filter response compared with those of sharp cutoff Chebyshev filters
The roll-off response of the DSP-based filter is much closer to the response of an ideal filter. The analog filters can be improved; however, achieving the same response as the digital system would be cost-prohibitive. Each added analog stage could also generate unwanted artifacts, such as phase shift. Additionally, complex analog filters are less stable over time compared to DSP-based filters, which will always achieve the exact same response.
What is an FIR filter?
An FIR (Finite Impulse Response) filter is a type of digital filter used in signal processing to modify or analyze the characteristics of a digital signal. It's called "finite impulse response" because its output response is based on a finite number of input samples.
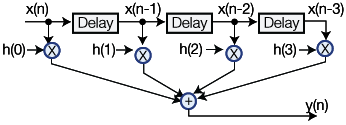
Figure 3: Block diagram of an FIR filter
Key characteristics of an FIR filter:
- Impulse Response: The impulse response of an FIR filter is the sequence of filter coefficients, which determines how the filter responds to an input signal containing an impulse (a single sample with value 1 followed by zeros).
- No Feedback: Unlike IIR (Infinite Impulse Response) filters, FIR filters do not have feedback loops in their design, making them inherently stable and avoiding issues such as instability and pole-zero cancellation.
- Linear Phase: FIR filters can be designed to have linear phase response, which means that all frequency components of the input signal experience the same delay, preserving the shape of the input signal.
- Symmetry: Some FIR filter designs, such as linear-phase filters, exhibit symmetry in their coefficients, making their frequency response symmetric around the center frequency.
- Design Flexibility: FIR filters can be designed to have specific frequency responses, such as low pass, high pass, bandpass, or band stop. This is done by carefully selecting their coefficients.
- Transversal Structure: FIR filters are often implemented using a transversal structure, where the input samples are multiplied by filter coefficients and then summed to produce the filtered output.
- Non-recursive: FIR filters do not involve recursive calculations or previous output samples in their operation, simplifying their implementation and reducing the potential for instability.
FIR filters find applications in various areas of signal processing, including:
- Audio Processing: Equalization, noise reduction, and digital audio effects
- Communication Systems: Pulse shaping, channel equalization, and interference rejection
- Image Processing: Image enhancement, noise reduction, and edge detection
- Biomedical Signal Processing: Filtering out noise from physiological signals
- Control Systems: Filtering sensor signals for control and feedback loops
Designing FIR filters involves selecting appropriate filter characteristics, such as filter type, cutoff frequencies, and passband/stopband ripple, and then using algorithms like windowing, frequency-sampling, or optimization methods to determine the filter coefficients that achieve the desired response.
What are some of the other advantages of digital vs analog?
In addition to its flexibility, DSP-based systems do not suffer from the noise that might be generated from analog components. The digital format is also more stable in terms of storage; as long as the storage medium does not fail, the data will never change or degrade over time. While many in the audio and video professions will tell you that analog signal processing achieves better results, there’s no debating the convenience and flexibility of DSP.
Sampling Real-World Signals for DSP
DSP systems acquire data in two ways: one sample at a time or one frame at a time. In a sample-based system, a sample is acquired, and a processed sample is output with each clock signal. The output waveform is developed continuously. Figure 4 illustrates a sample-based digital filter.

Figure 4: Continuous processing of samples in a digital filter
Frame-based systems acquire a block of samples, or a frame. The entire frame of data is processed and then output. Figure 5 illustrates a frame-based system, such as a spectrum analyzer, which determines the frequency components of a time-varying waveform.

Figure 5: Batch processing of a block of data
At a sample rate of 48 kHz, there is a sample every 20.833 µs. For a frame of 1024 samples, the processor has an acquisition interval of 21.33 ms, meaning that all processing must take place in that time. In a real-time system, data cannot be lost, so while the first frame is being processed, the next frame must be acquired at the same time.
Not all of the 21.33 ms can be used for processing, however, the DSP’s response time must also be accounted for. External devices, such as an analog-to-digital converter (ADC) signal the processor via an interrupt. The DSP’s response time to the interrupt is called interrupt latency. A DSP’s interrupt latency is dependent on many things, the most dominant being the number of instruction cycles that occur between receiving an interrupt and resuming execution, or instruction pipeline. The more cycles there are, the longer the interrupt latency. A processor with a 20 ns cycle time and requires 10 cycles to respond to an interrupt will need 200 ns before it executes any instructions. These cycles add up, especially with frame-based systems. To avoid wasted cycles, many DSPs have architectural features, such as direct-memory access (DMA) and dual memory access, which enable the DSP to receive and store data without interrupting the processor.
What’s in a complete DSP system?
A typical DSP system consists of just a few components, as illustrated in Figure 6.

Figure 6: Block diagram of an example DSP system
The analog signal is bandwidth-limited by the anti-aliasing filter before entering the ADC. The ADC converts the analog signal to digital and sends it to the DSP. The DSP processes the data and sends it to the digital-to-analog converter (DAC). The resulting analog signal is smoothed by an anti-imaging (or reconstruction) filter. In some systems, the DSP communicates with a host interface, which handles sending and receiving data and control information. Every component is connected to a clock oscillator. In many modern systems, the ADC, DAC, clock, and filters are combined into one IC.
How to model filter transform functions
To model a filter, the process must be first broken down into mathematical steps. The mathematical steps, along with any other required operations, can be translated to software. Typically, this software is written in a high-level language, such as C. The following code performs the previously discussed FIR filter.
float *hist_ptr, *hist1_ptr, *coef_ptr;
float output;
hist_ptr = history;
hist1_ptr = hist_ptr; /* use for history update */
coef_ptr = coef + n -1; /* point to last coef */
/*form output accumulation */
output = *hist_ptr++ * (*coef_ptr-);
for(i = 2; i < n; i++) {
*hist1_ptr++ = *hist_ptr; /* update history array */
output += (*hist_ptr++) * (*coef_ptr-); } output += input * (*coef_ptr); /* input tap */ *hist1_ptr = input; /* last history */ return(output); }
While coding in a high-level language is commonplace (and many available pre-coded libraries and solutions are developed for high level languages), coding in a low-level language, such as Assembly, can optimize system performance, as well as help with understanding a DSP’s architecture.
What is the architecture of a DSP?
In general, there are four relevant sections of DSP architecture when understanding programming: numeric, memory, sequencer, and I/O operations.
Numeric: What distinguishes a DSP from more general-purpose microprocessors is hardware that is optimized for numeric operations. DSPs contain a multiply/accumulator (MAC), an arithmetic-logic unit (ALU), and a barrel shifter. Sum-of-products operations, which appear in most DSP algorithms, including FIR filters, are performed by the MAC. The ALU performs addition, subtraction, and logical operations. Operations on bits and words are processed by the barrel shifter.
Dedicated hardware for numeric operations provides a great deal of flexibility and efficiency. Non-conflicting data paths allow for parallel processing. Because arithmetic operations increase word length, the architecture of the DSP must provide a wide dynamic range to prevent overflow.
Memory: The memory and bus architecture of a DSP are designed for speed. Most microprocessors use a single memory space which stores both data and instructions. This is known as the von Neumann architecture. On the other hand, a DSP’s memory is typically divided into program and data memory, each with its own bus. With this separation, DSPs can access multiple pieces of data on each cycle, increasing throughput. This is referred to as the Harvard architecture.
DSPs use specialized data-address generators (DAGs) to reduce the number of instructions required to manage memory accesses. Because most DSP algorithms fetch data from memory in a repeated pattern of accesses, any additional instructions (or overhead) can lead to wasted cycles. DSPs have two DAGs; one address generator generates an address over the data-memory address bus, while the other generates an address over the program-memory bus. Most DSP algorithms require two operands as the inputs to the arithmetic units. Two DAGs enable the two operands to be fetched from memory in a single cycle.
Many DSP algorithms require a buffer, a range of addresses where data is stored, where the address pointer “wraps around” to the beginning once it reaches the end. This wrapping around is called circular buffering. Some algorithms require the address pointer to advance more than one address per step, but still must wrap around to the beginning when it reaches the end. This variation is called modulo circular buffering. Figure 7 illustrates an example of modulo circular buffering, where the pointer skips two addresses as it advances.

Figure 7: Modulo Circular Buffering. Image Source: Analog Devices
Sequencer: Most DSP algorithms are repetitive and the code describing them contains a loop. In a microprocessor, program loops are typically maintained in software, where a conditional instruction at the end of the loop determines whether the address pointer jumps back to the top of the loop or moves on to another address. Retrieving these addresses takes time, and a DSP reduces this time by performing these test and branch functions in hardware, storing the needed addresses.

Figure 8: Example of a program loop. Image Source: Analog Devices
Figure 8 illustrates a program loop as performed by a DSP. All addresses are stored by hardware as the loop runs, eliminating the need to retrieve addresses. Additionally, operations evaluating conditionals and branching program execution are all performed by dedicated hardware, reducing overhead.
Input/Output (I/O): DSPs are designed for large throughput of data and have a variety of inputs and outputs, including serial ports, I/O ports, and direct memory accessing (DMA) channels.
How to implement a digital filter in Assembly language
To illustrate the steps that a DSP might take when executing a process, the FIR filter has been coded into Assembly. This example is specific to the Analog Devices ADSP-2181, a fixed-point, 16-bit DSP. The code has two parts: a main routine, which includes register and buffer initialization, and an interrupt routine that executes when there is a data sample. The last segment of code is the interrupt subroutine. When the interrupt is received, the processor jumps to this routine, processing the input sample. After processing, the output is sent to the D/A converter.
/******** Initialize Constants and Variables *****************/
.const taps=127;
.var/dm/circ data[taps];
.var/pm/circ fir_coefs[taps];
.init fir_coefs: ;
.var/dm/circ output_data[taps];
/******** Interrupt vector table *****************************/
reset_svc: jump start; rti; rti; rti;
/*00: reset */
irq2_svc: /*04: IRQ2 */
si=io(0); /* get next sample */
dm(i0,m0)=si; /* store in tap delay line */
jump fir; /* jump to fir filter */
nop; /* nop is placeholder */
irql1_svc: rti; rti; rti; rti; /*08: IRQL1 */
irql0_svc: rti; rti; rti; rti; /*0c: IRQL0 */
sp0tx_svc: rti; rti; rti; rti; /*10: SPORT0 tx */
sp0rx_svc: rti; rti; rti; rti; /*14: SPORT1 rx */
irqe_svc: rti; rti; rti; rti; /*18: IRQE */
bdma_svc: rti; rti; rti; rti; /*1c: BDMA */
sp1tx_svc: rti; rti; rti; rti; /*20: SPORT1 tx or IRQ1 */
sp1rx_svc: rti; rti; rti; rti; /*24: SPORT1 rx or IRQ0 */
timer_svc: rti; rti; rti; rti; /*28: timer */
pwdn_svc: rti; rti; rti; rti; /*2c: power down */
/******* START OF PROGRAM - initialize mask, pointers **********/
start:
/* set up various control registers */
ICNTL=0x07; /* set IRQ2, IRQ1, IRQ0 edge sensitive */
IFC=0xFF; /* clear all pending interrupts */
NOP; /* add nop because of one cycle */
/* synchronization delay of IFC */
SI=0x0000;
DM(0x3FFF)=SI; /* sports not enabled */
/* sport1 set for IRQ1, IRQ0, FI, FO */
IMASK=0x200; /* enable IRQ2 interrupt */
i0=^data; /* index to data buffer */
l0=taps; /* length of data buffer */
m0=1; /* post modify value */
i4=^fir_coefs; /* index to fir_coefs buffer */
l4=taps; /* length of fir_coefs buffer */
m4=1; /* post modify value */
i2=^output_data; /* index to data buffer */
l2=taps; /* length of data buffer */
cntr=taps;
do zero until ce;
dm(i0,m0)=0; /* clear out the tap delay data buffer */
zero: dm(i2,m0)=0; /* clear out the output_data buffer */
/**** WAIT for IRQ2 Interrupt - then JUMP to INTERRUPT VECTOR **/
wait: idle; /* wait for IRQ2 interrupt */
jump wait;
/******* FIR FILTER interrupt subroutine ***********************/
fir cntr=taps-1; /* set up loop counter */
mr=0, mx0=dm(i0,m0), my0=pm(i4,m4);
/* fetch data and coefficient */
do fir1loop until ce; /* set up loop */
fir1loop: mr=mr+mx0*my0(ss), mx0=dm(i0,m0), my0=pm(i4,m4);
/* calculations */
/* if not ce jump fir1loop;*/
mr=mr+mx0*my0(rnd); /* round final result to 16-bits */
if mv sat mr; /* if overflow, saturate */
io(1)=mr1; /* send result to DAC */
dm(i2,m0)=mr1;
rti;
/******* END OF PROGRAM *************************************/
.endmod;
4. Applications
What are the applications of DSP?
Digital Signal Processing (DSP) is a very power tool that is used in a wide range of applications across various domains. The following are some common applications of DSP:
Telecommunications: DSP plays an important role in modern telecommunications systems, including voice and data transmission, error correction, modulation, and demodulation.
Audio Processing: DSP is extensively used in audio applications, including audio compression (e.g., MP3), noise reduction, equalization, and audio effects processing. It's also found in music production, digital audio players, and voice recognition systems.
Image Processing: DSP is used for image enhancement, compression, and analysis. It's employed in medical imaging (MRI, CT scans), digital cameras, facial recognition, and image and video compression standards (JPEG, MPEG).
Radar and Sonar Systems: DSP is used to process radar and sonar signals to detect and track objects, determine their distance, speed, and direction, and reduce clutter and noise.
Biomedical Signal Processing: In healthcare, DSP is used for processing and analyzing signals from various medical instruments, including ECG (Electrocardiogram), EEG (Electroencephalogram), and MRI scans. It aids in disease diagnosis and monitoring.
Speech and Audio Compression: DSP is essential in speech coding and audio compression algorithms, which are used in applications like VoIP (Voice over Internet Protocol) and audio streaming services.
Seismic Data Analysis: DSP helps in the analysis of seismic signals for earthquake detection and characterization of subsurface structures in geophysical exploration.
Astronomy and Astrophysics: DSP techniques are used in radio astronomy to analyze and process signals from radio telescopes, helping scientists study celestial objects and cosmic phenomena.
Control Systems: DSP is used in control applications to process feedback signals and control actuators in real-time for systems like robotics, automotive engine control, and industrial automation.
Wireless Communication: In wireless communication systems, DSP is used for channel equalization, error correction, and adaptive modulation to ensure reliable data transmission in changing wireless environments.
Environmental Monitoring: DSP aids in processing data from sensors in environmental monitoring systems, including weather prediction, pollution measurement, and forest fire detection.
Financial Signal Processing: DSP is used in financial markets for algorithmic trading, risk assessment, and data analysis to make informed investment decisions.
Biometric Systems: DSP is employed in biometric systems for fingerprint recognition, face recognition, and iris scanning.
Smart Grids: DSP is used to process data from sensors and meters in smart grids, enabling efficient energy distribution and consumption management.
These are just a few examples, and the applications of DSP are continually expanding as technology advances. DSP is a fundamental tool in the modern world, enabling the efficient processing and analysis of a wide range of signals and data in various industries and scientific fields.
6. Glossary
- Analog-digital converter (ADC):a device that converts continuous analog signals into discrete digital values for processing and storage in digital systems
- Arithmetic-logic unit (ALU): a component that performs arithmetic and logical operations on data. It's the "computational engine" of a processor.
- Bandpass filter: A filter that allows a specific range of frequencies, known as the passband, to pass through while attenuating others
- Digital-analog converter (DAC): a device that converts digital signals into continuous analog signals, often used to produce audio or control analog systems
- FIR filter: a digital filter with a finite-length impulse response, used for signal processing tasks like smoothing and noise reduction.
- Fixed-point: a system that represents numbers with a consistent number of integer and fractional bits for arithmetic operations
- Floating-point: a system that uses a dynamic exponent and mantissa to represent numbers with varying precision for complex calculations
- Impulse response: the reaction of a dynamic system at the output when presented with a brief input signal or change in an input signal
- Modulo: a math operation that returns the remainder when two integers are divided
- Recursive filter: a filter in which the current output is dependent on previous outputs and inputs
- SHARC (Super Harvard Architecture Single-Chip Computer): a high performance floating-point and fixed-point DSP from Analog Devices
*Trademark. Analog Devices is a trademark of Analog Devices, Inc. Other logos, product and/or company names may be trademarks of their respective owners.
For more DSP products Shop Now
Test Your Knowledge
DSP 1

Complete our Essentials: DSP 1 course and take the quiz to earn this badge.
Are you ready to demonstrate your wind power knowledge? Then take a quick 10-question multiple choice quiz to see how much you've learned from this module.
To earn the Essentials Power 6 Badge, read through the learning module and attain 100% in the quiz.









