You cannot always trust AIs
I asked four major AI chat bots the same question:
"What is the most efficient way to implement IIR filters? Reply in 40 words or less."
Here are the responses:
Perplexity AI:
"Use a cascade of second-order (biquad) sections in Direct Form II for IIR filter implementation. This approach ensures computational efficiency, numerical stability, and is suitable for both software and hardware, especially when paired with careful scaling and quantization."
ChatGPT 4:
"The most efficient way to implement IIR filters is using Direct Form II Transposed structure, which minimizes memory usage and improves numerical stability by reducing the number of delay elements and limiting quantization noise propagation."
Claude Sonnet 4:
"Use Direct Form II (transposed) structure for best numerical stability and minimal memory. Implement with fixed-point arithmetic on embedded systems or floating-point for general use. Cascade second-order sections for higher-order filters to reduce quantization errors."
Grok 4:
"The most efficient way to implement IIR filters is using direct form II transposed structure, minimizing memory and computational complexity with biquad sections, optimized coefficients, and fixed-point arithmetic for real-time processing on DSPs or microcontrollers."
All of them recommend the Direct Form II using a biquad cascade architecture and all of them are completely wrong. By a factor of 2.5x.
An IIR filter of order N will require 2.5N multiplications/output sample when implemented with a biquad cascade (every byquad has order 2 and uses 5 multiplications). This architecture also suffers from all the drawbacks mentioned in an earlier post, potential instability, coefficient quantization sensitivity issues, limit cycles, very difficult to pipeline, etc.
A much better architecture is a Lattice Wave Digital Filter structure, a 2-phase polyphase decomposition, with two branches implemented as cascades of second order all-pass sections, which I will describe in greater detail in a future post. An LWDF IIR filter of order N only needs N multiplications and there is even a bireciprocal version, very similar to FIR half-band filters, where half of the coefficients are zero, so only 0.5N multiplications/output sample.
The most common topology for all pass sections is called Richards, coming from microwave transmission line theory. There are two equivalent discrete implementations, Type 1 and Type 2. They are functionally equivalent and differ only in the numerical rounding noise propagation as a function of the coefficient value.
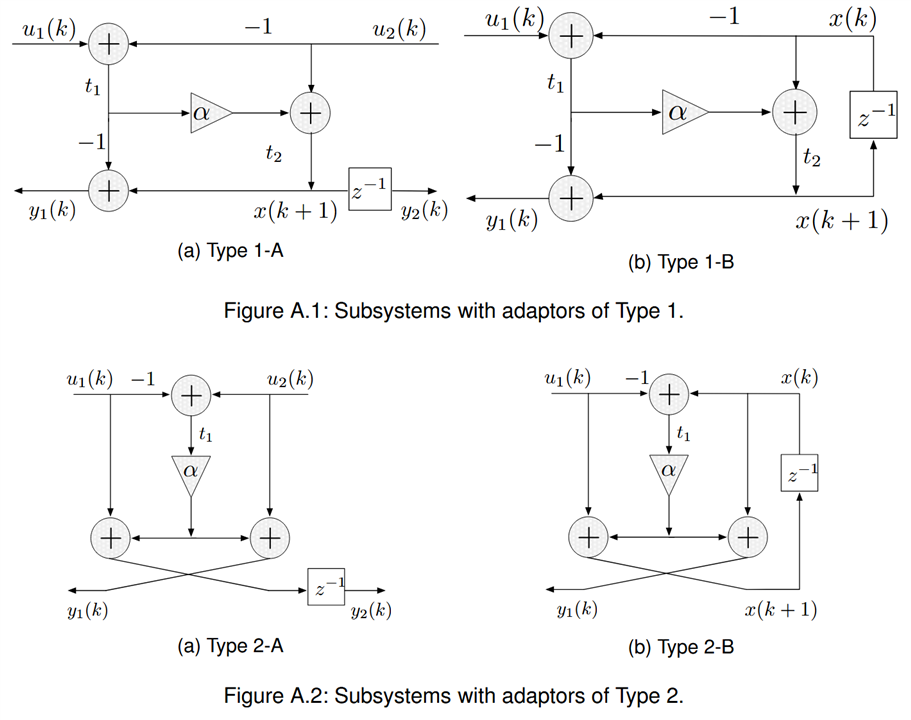
Type 1-B and 2-B can be used as first order all pass sections and cascading A and B Types creates a second order all pass section. Cascading second order sections and optionally one first order section if N is odd can create an all pass IIR filter of any order N. So the first and second order all-pass sections using this Richards topology look like this:
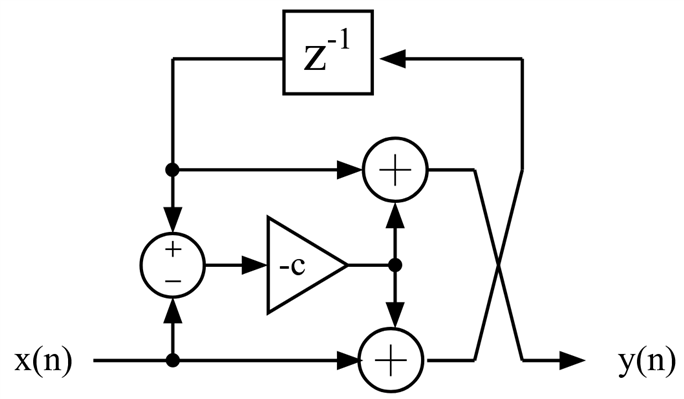
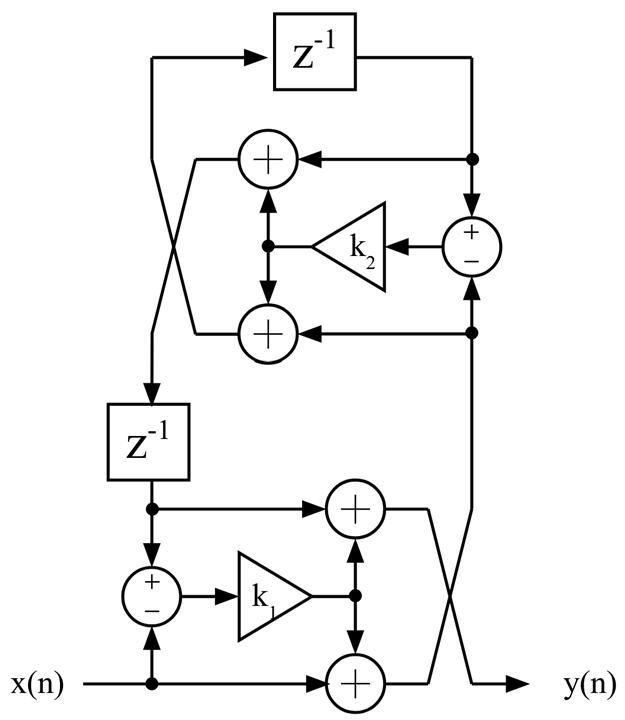
The problem with these all pass building blocks is that they minimize the number of delays at the cost of extra adders. A second order Richards all pas section has two multiplications, two delays and six additions. For an FPGA implementation this is suboptimal, we would like to use two DSP primitives and no fabric adders, which means two multipliers and four adders. Fortunately, there is an alternate all pass section implementation, which only uses two multipliers and four adders, at the cost of more delays, which is not a problem for an FPGA implementation. Here are how the first and second order sections look like:

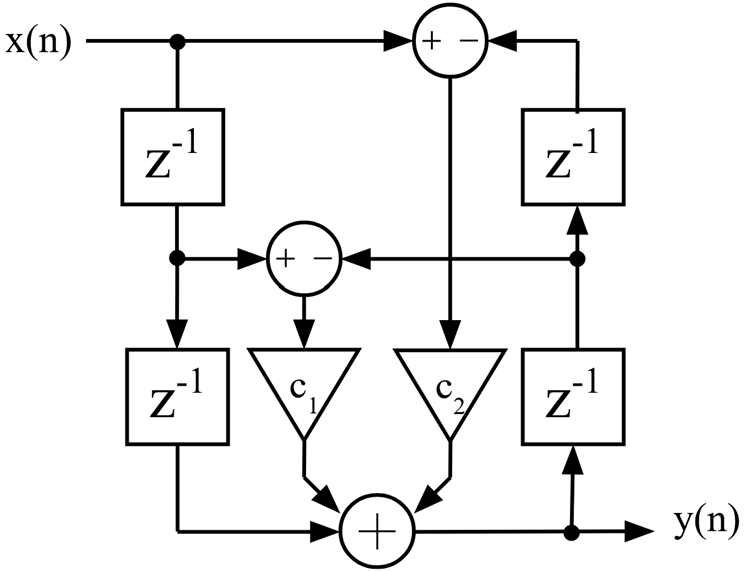
and these are their H(z) transfer functions and the conditions for stability:

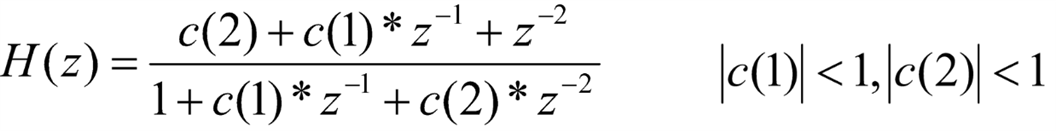
In general we also want to consider a packing factor n, where we replace every delay with n delays and z-1 becomes z-n in all formulas above.
The magnitude of the transfer function is obviously always 1.0, that's what all pass filters are all about. Calculating the phase of the transfer function is relatively easy but I drew the line at manually computing the derivative for the group delays. So I used the free Mathematica Online tool to calculate that for both first and second order all-pass sections with a packing factor n:

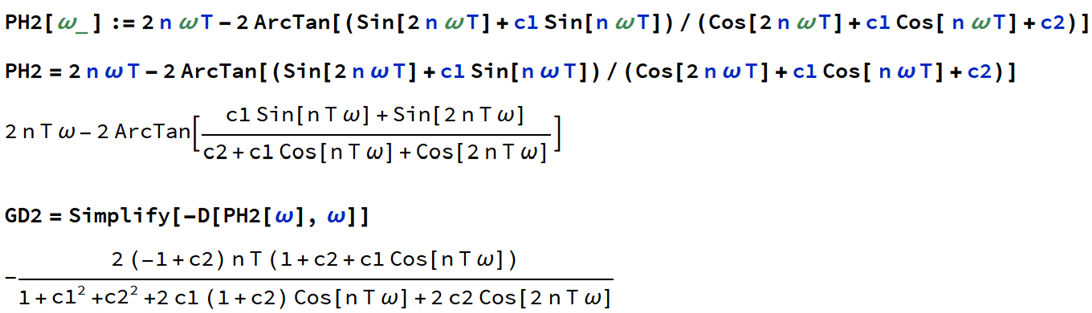
We can now use these formulas to compute both the phase and the group delay at any frequency f. Since a cascade of all pass sections is still all pass, both its phase and group delay are the sums of individual sections phases and group delays and we can use that to analyze any IIR filter built with first and second order sections. .
In the next posts, I will show first how to pipeline the first and second order all pass blocks so that they fit efficiently into DSP primitives and run at the maximum possible clock frequency. Next we will see how these efficient all pass sections can be used to implement many types of IIR filters, including almost linear phase ones.
In conclusion, there is no reason one should use biquad cascades, the LWDF architecture is superior in every way.
To close on the whole AI subject and for full disclosure, I used Perplexity.AI to come up with the correct Mathematica syntax.
Back to the top: The Art of FPGA Design Season 2

Top Comments