Linear Phase IIR Filters? Part 2

The forward-backward method of turning any non-linear phase IIR into a "linear phase" one at a much lower hardware cost than the classic linear phase FIR implementation I showed in the previous blog post works great if you do not mind the large increase in latency. But what can be done if only approximate linear phase is needed but with a much lower latency? 

Well, LWDF IIR filters can do that too. Remember that such a filter has an architecture like this: 

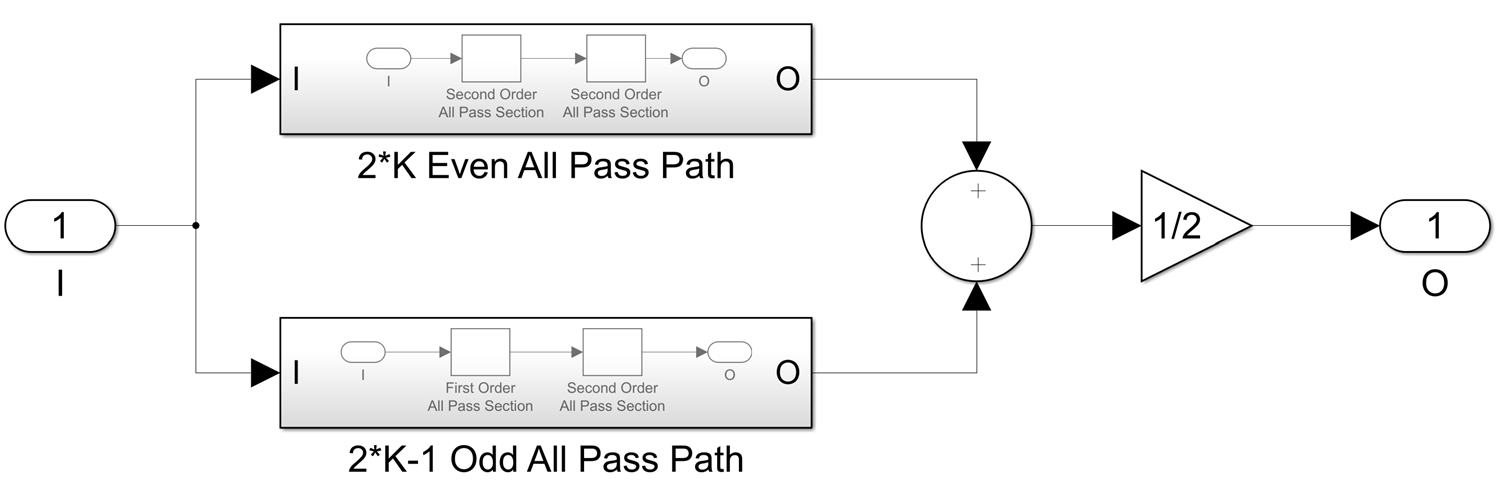
It works by choosing coefficients in such a way so the phases of the two branches match each other very well in the pass band but are offset by 180 degrees in the stop band. The trick for achieving almost linear phase is to force every single coefficient in the odd branch to zero, then it effectively becomes a 2*K-1 delay and all delays have a linear phase transfer function. The even branch will be forced now to be very close to linear phase by constraining the pass band amplitude ripple - the less ripple you have, the closer the phase in the frequency band will be to linear. 

Of course, there are no filters with a perfectly flat pass band, IIR or otherwise, so the phase of the resulting filter, which is the average of the phases of the two branches, will be almost linear. We can get as close as we want with a higher order filter but only in an asymptotic sense. And there is a price to be paid too, these "linear phase" IIRs have at least twice the order of non-linear Cauer (Elliptic) filters with similar amplitude transfer functions. Depending on the order of the FIR we want to replace (the larger the better) and the group delay ripple (the lower the harder it becomes), significant savings relative to a direct equiripple FIR implementation are still possible. 

This type of filters is very well explained in fred harris's book Multirate Signal Processig for Communication Systrems, Second Edition which I highly recommended. The best $50 you can ever spend if you are into DSP. Chapter 11, Recursive Polyphase Filters is dedicated to this very subject. It even provides a Matlab tool to design such filters, and I used it to create a "linear phase" version of the second example IIR filter from Post 24. The specs were FS=1000MHz, f_p=240MHz, a_p<0.1mdB, f_s=260MHz and a_s=100dB. An Elliptic bireciprocal IIR filter of order 21, that used 10 multiplications met these requirements but its phase was highly non-linear. The equivalent equiripple half-band FIR design had of course linear phase but its order was N=303 and required 76 multipliers. 

Rather than designing a single "linear phase" IIR filter with these specs, it is easier to design the square root filter and cascade two such filters. So here are the settings for a filter with half the passband ripple and half the stop band attenuation, which can be implemented with 24 multiplications. Here is the stop band transfer function: 

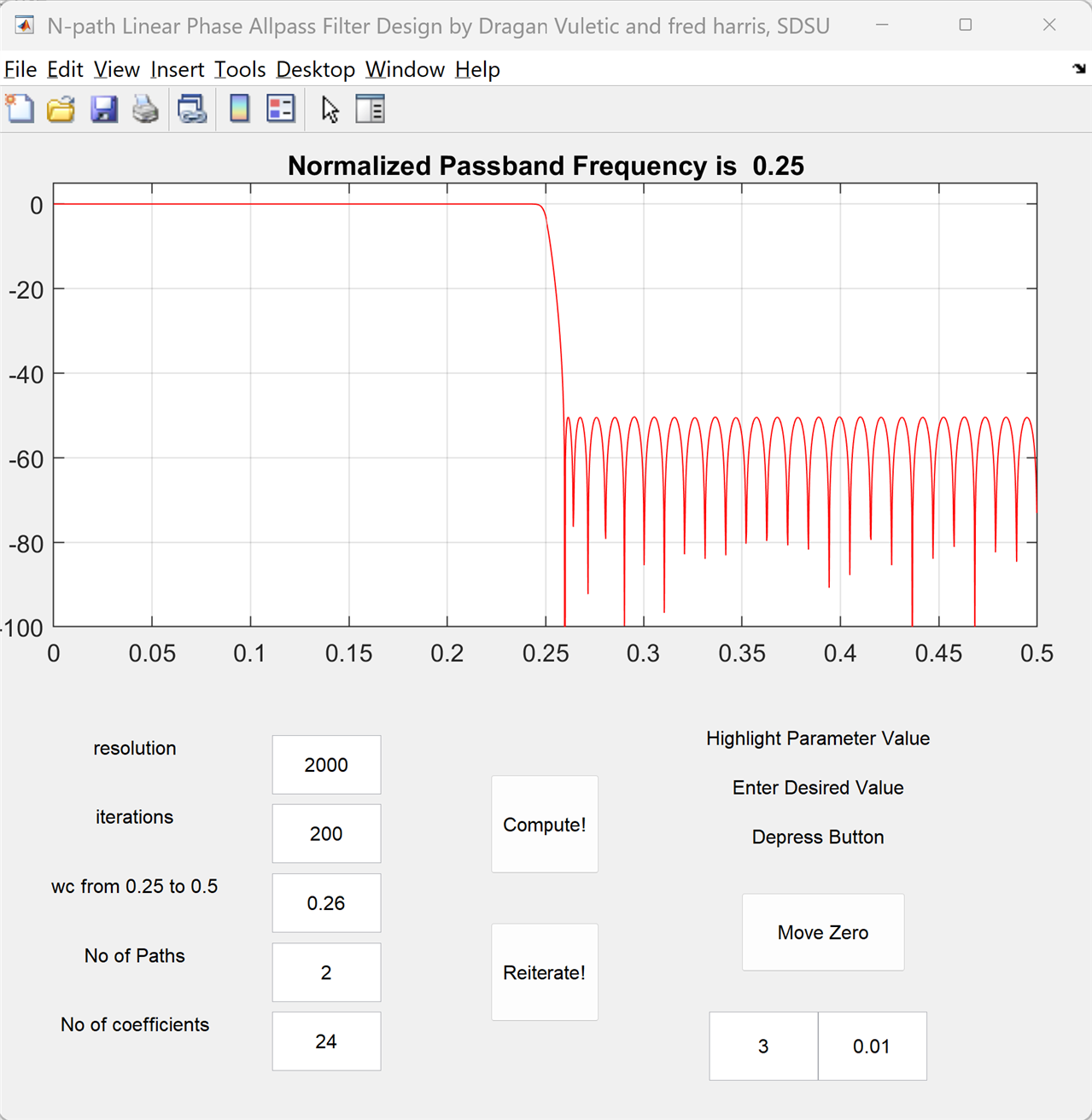
the pass band ripple: 

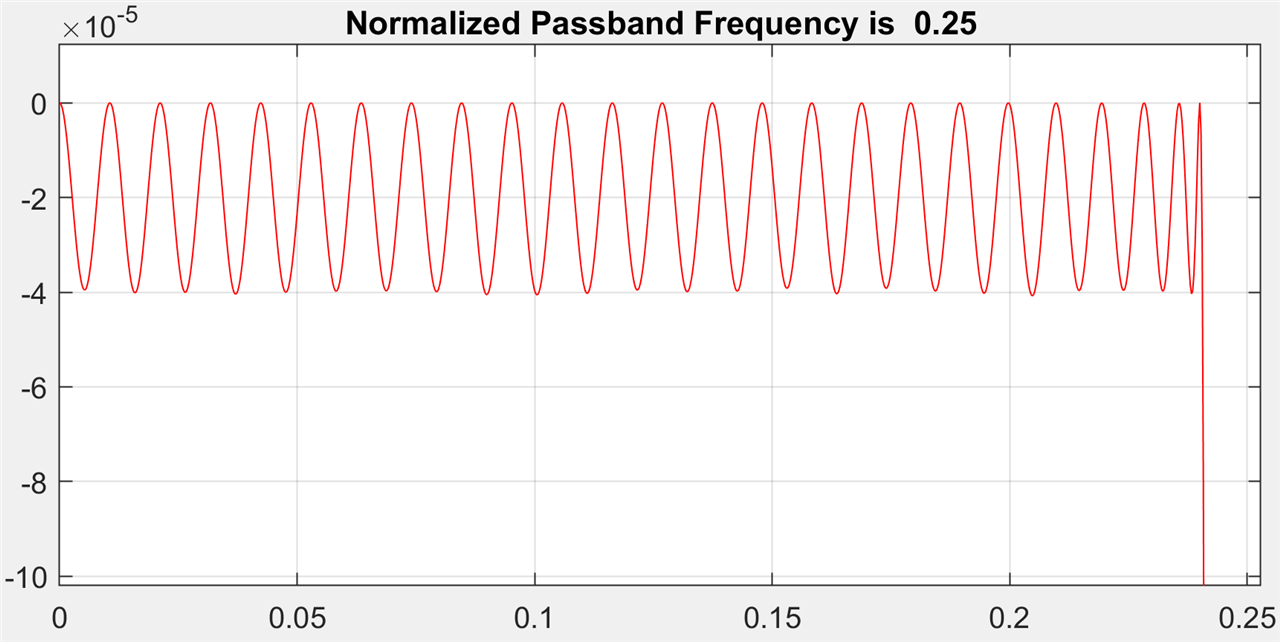
and the pass band group delay ripple: 

The transfer function of the two cascaded filters is: 

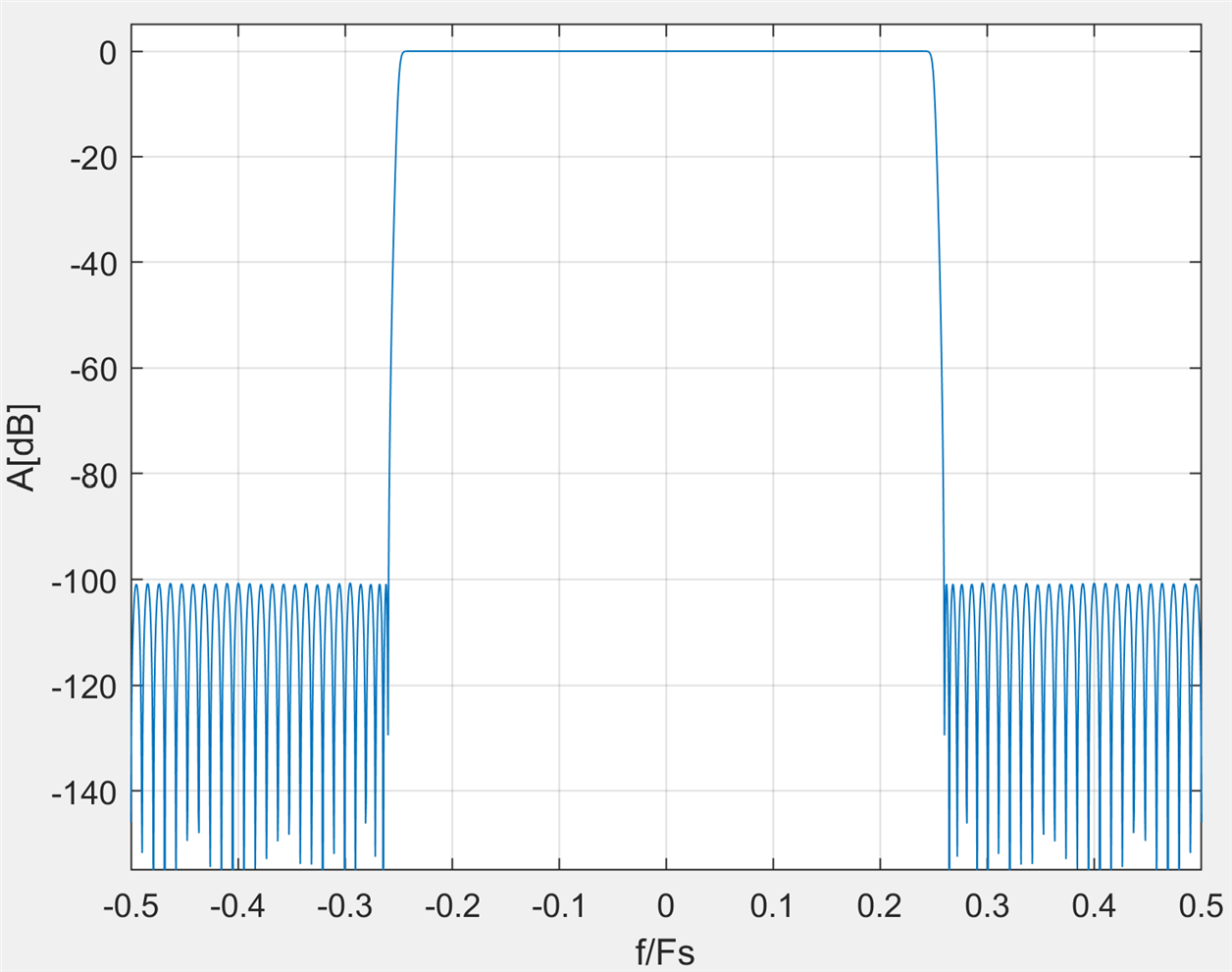
 the pass band ripple also meets the specs: 

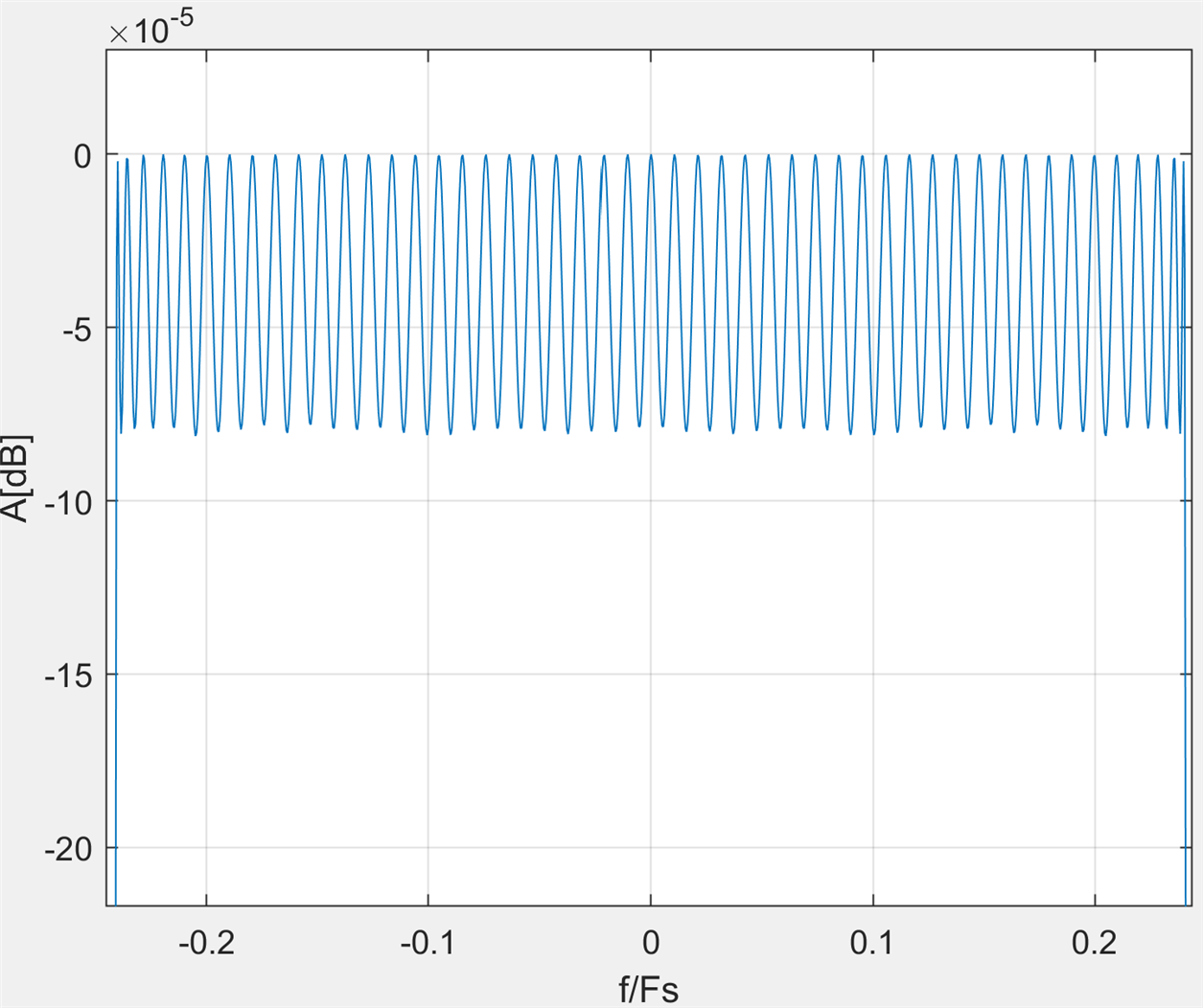
and this is the group delay ripple: 

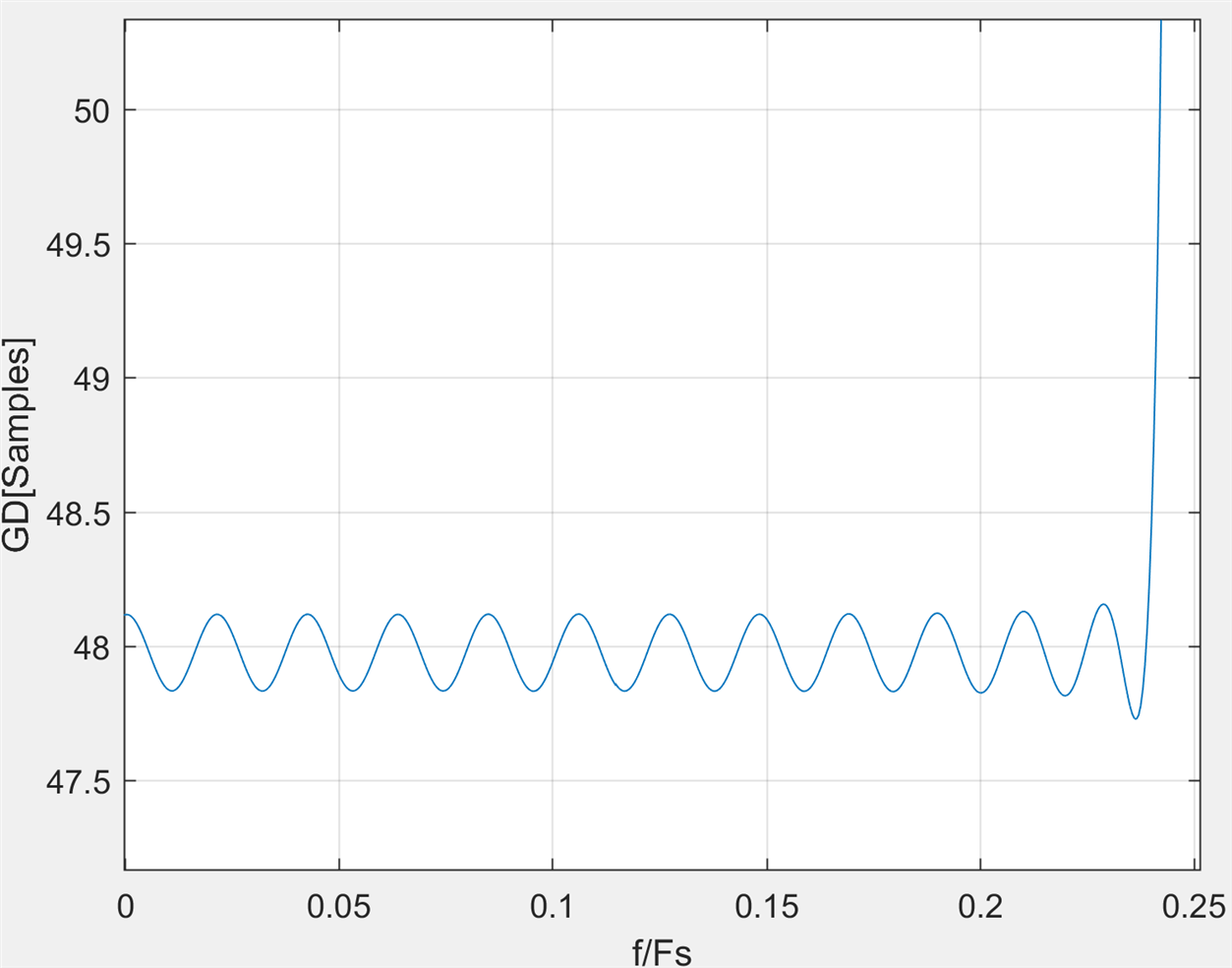
The final design uses 48 multipliers, this is still 1.58x smaller than the equivalent FIR. 

In conclusion, if the extra latency of the forward-backward method is unacceptable but some group delay ripple can be tolerated, there is a second way to address the problem of the high phase non-linearity of IIR filters. 

Back to the top: The Art of FPGA Design Season 2